Джордан Элленберг - Как не ошибаться. Сила математического мышления

Это возвращает нас к вопросу о Творце Вселенной.

Самый знаменитый аргумент в пользу сотворения этого мира Богом – это так называемый аргумент о замысле, который в самой простой его форме сводится к следующему: вы только посмотрите вокруг , неужели вы считаете, что настолько сложный и удивительный мир мог сформироваться всего лишь по воле случая и физических законов?

Более формально этот принцип сформулировал либеральный теолог Уильям Пейли в опубликованной в 1802 году книге Natural Theology; or, Evidences of the Existence and Attributes of the Deity, Collected from the Appearances of Nature («Естественная теология, или Свидетельства существования Бога и Его атрибутов, собранных из явлений природы»):

Пересекая луг, я, предположим, ударился ногой о камень , и, если бы меня спросили, как этот камень оказался там, я, наверное, ответил бы, что, насколько мне известно, он всегда там лежал. И было бы нелегко показать абсурдность такого ответа. Но, предположим, я нашел на земле часы , и, если бы потребовалось узнать, как часы оказались в этом месте, мне вряд ли бы пришло на ум дать такой же ответ, как и в предыдущем случае – мол, насколько мне известно, часы скорее всего всегда были там. Почему же такой ответ не подходит к случаю с часами так же, как к случаю с камнем? Почему он во втором случае не приемлем, как приемлем в первом? По той единственной причине, что когда мы начинаем изучать часы, то видим (чего мы не могли видеть в камне), что составные части часов изготовлены и собраны воедино для определенной цели, то есть они созданы и приспособлены так, чтобы производить движение, а это движение отрегулировано так, чтобы показывать, который сейчас час… Вывод, мы думаем, неизбежно таков, что у часов был создатель: в какое-то время и в каком-то месте должен был существовать мастер или мастера, создавшие их для той цели, которой они соответствуют; мастер или мастера, которые знали устройство часов и продумали, как их использовать (курсив Ричарда Суинберна. – Ред .) [158].

Если это истинно в отношении часов, то насколько более это истинно в отношении воробья, или человеческого глаза, или человеческого мозга?

Книга Пейли имела огромный успех: она была издана пятнадцать раз за пятнадцать лет {151}. Дарвин, который внимательно прочитал ее в колледже, сказал впоследствии: «Думаю, что я никогда не восхищался книгой больше, чем книгой Пейли “Естественная теология”: в прошлом я мог пересказать ее наизусть» {152}. А усовершенствованные разновидности аргумента Пейли образуют основу современного движения в поддержку концепции разумного замысла.

Разумеется, это классическое доказательство от маловероятного:

• если Бога нет, существование таких сложных объектов, как человеческие существа, было бы маловероятным;

• люди существуют;

• следовательно, маловероятно, что Бога нет.

Напоминает аргументацию, которую использовали искатели библейских кодов: если Бог не писал Тору, маловероятно, чтобы в тексте на свитке были столь точные записи имен и дат рождения раввинов!

Наверное, вам уже надоело, что я так часто это повторяю, но доказательство от маловероятного работает не всегда. Если мы действительно хотели бы представить в количественном выражении степень своей уверенности в том, что Бог создал Вселенную, нам следовало бы нарисовать другую байесовскую матрицу.

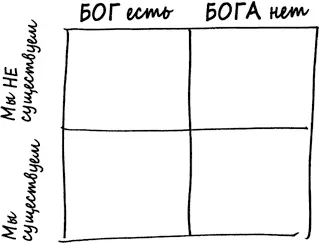
Первая трудность состоит в том, чтобы определить априорные вероятности. Сделать это довольно трудно. В случае рулетки мы задавали такой вопрос: какую вероятность мы присваиваем предположению, что колесо рулетки не работает надлежащим образом, прежде чем увидим его вращение? Теперь мы ставим вопрос так: какую вероятность мы присвоили бы гипотезе о существовании Бога, если не знали бы о существовании Вселенной, Земли и себе подобных?

В этот момент самым естественным шагом было бы развести руками и прибегнуть к принципу с очаровательным названием «принцип безразличия». Поскольку не существует принципиального способа сделать вид, что мы не знаем о собственном существовании, нам остается просто разделить априорную вероятность поровну, присвоив 50 % теории, что Бог есть, и 50 % – теории, что Бога нет [159].

Если истинна теория, что Бога нет, тогда столь сложные существа, как люди, должны были возникнуть по чистейшей случайности, чему, возможно, способствовал естественный отбор. Сторонники концепции разумного замысла сходятся во мнении, что подобное крайне маловероятно; давайте выразим все в числах и скажем, что эта вероятность составляет один шанс на миллиард миллиардов. Следовательно, в нижней правой клетке матрицы мы запишем одну миллиардмиллиардную от 50 %, или одну двухмиллиардмиллиардную.