Джордан Элленберг - Как не ошибаться. Сила математического мышления

Если истинна гипотеза имитации и Вселенная представляет собой модель, сконструированную людьми в более реальном мире, тогда вполне вероятно, что в этой Вселенной будут люди, поскольку люди любят имитировать людей! Я назвал бы это почти полной уверенностью (для целей нашего примера давайте говорить об абсолютной уверенности) в том, что в имитационном мире, созданном технологически развитым человечеством, будут (смоделированные) люди.

Если мы присвоим каждой из четырех гипотез, о которых шла речь выше, априорную вероятность 1/4, матрица будет выглядеть так.

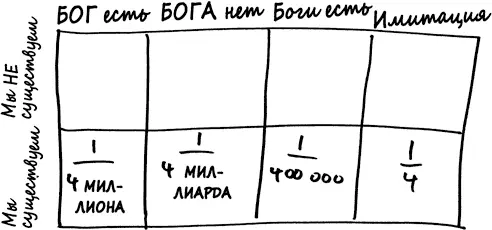
Учитывая тот факт, что мы все-таки существуем, истина находится где-то в нижней строке матрицы, но наибольшая вероятность – в клетке имитация . Да, существование человеческой жизни – это доказательство существования Бога, однако гораздо лучшее доказательство состоит в том, что наш мир был запрограммирован людьми, которые намного умнее нас.

Сторонники так называемого научного креационизма утверждают, что во время школьных занятий мы должны рассказывать о существовании создателя этого мира, но не потому, что так гласит Библия (это было бы просто непозволительно!), а по веским причинам, основанным на поразительной маловероятности существования человечества при условии истинности гипотезы, что Бога нет.

Но, если бы мы всерьез отнеслись к такому подходу, мы рассказывали бы десятиклассникам нечто в таком роде:

Некоторые утверждают, будто в высшей степени маловероятно, чтобы нечто столь сложное, как биосфера Земли, возникло сугубо в процессе естественного отбора без какого бы то ни было вмешательства извне. Вне всяких сомнений, самым вероятным объяснением является то, что на самом деле мы не физические существа, а обитатели компьютерной модели, выполненной людьми с намного более развитой технологией. Правда, с какой целью – мы точно не знаем. Возможно также, что мы созданы сообществом богов, похожих на тех богов, которым поклонялись древние греки. Еще больше людей верят в то, что один Бог создал Вселенную, но эту гипотезу следует считать менее обоснованной, чем другие гипотезы.

Думаете, школьному совету это понравилось бы?

Тогда мне лучше поспешить и обратить ваше внимание на следующее: на самом деле гипотеза, что все мы компьютерные модели {154}, нравится мне не больше, чем аргумент Пейли о существовании Бога. Напротив, у меня возникло неприятное ощущение, будто эти аргументы свидетельствуют, что мы достигли предела количественного мышления. Мы привыкли выражать свою неуверенность в отношении чего-то в виде числа. Порой в этом даже есть свой смысл. Когда метеоролог говорит в вечерних новостях: «Завтра будет дождь с вероятностью 20 %», – это означает, что из всего множества прошедших дней с условиями, напоминающими текущие условия, в 20 % случаев на следующий день были дожди. Но что мы можем иметь в виду под фразой: «Вселенную создал Бог с вероятностью 20 %»? Это не может означать, что Бог создал одну вселенную из пяти, а остальные возникли сами по себе. Дело в том, что я так и не нашел метод, который показался бы мне вполне подходящим для присвоения числовых значений нашей неопределенности в отношении важнейших вопросов такого рода. Как бы я ни любил числа, я считаю, что люди должны придерживаться какого-то из принципов: «Я не верю в Бога», «Я верю в Бога» или просто: «Я не уверен». Как бы я ни любил байесовский вывод, я считаю, что людям лучше обретать веру (или отбрасывать ее), не прибегая к числам. В этом деле математика хранит молчание.

Если не верите мне, поверьте Блезу Паскалю, математику и философу, написавшему в XVII столетии:

Бог или есть, или Его нет; но на какую сторону мы склонимся? Разум тут ничего определить не может [162].

Но это еще не все. Паскаль много что успел сказать в своих «Мыслях» (Pensées). В следующей главе мы обратимся и к его труду и его размышлениям по этому вопросу. Но сначала поговорим о лотерее.

Студенты MIT обыгрывают лотерею штата Массачусетс

Как разбогател Вольтер

Геометрия флорентийской картины

Передача сообщений, исправляющих самих себя

Разница между Грэгом Мэнкью и Фран Лебовиц

«Извините, вы сказали “bofoc” или “bofog?”»

Салонные игры во Франции XVIII столетия

Где пересекаются параллельные прямые

Еще одна причина известности Дэниела Эллсберга