Джордан Элленберг - Как не ошибаться. Сила математического мышления

Но что если истинна теория, что Бог есть? Существует много вариантов того, в чем может быть выражено существование Бога; мы не знаем заранее, стал бы Бог, сотворивший Вселенную, создавать людей или любых других мыслящих существ, но любой Бог непременно обладал бы способностью сотворить разумную жизнь. Возможно, если Бог есть, существует один шанс на миллион, что Он создал бы таких существ, как мы.

Таким образом, наша матрица выглядит теперь так.

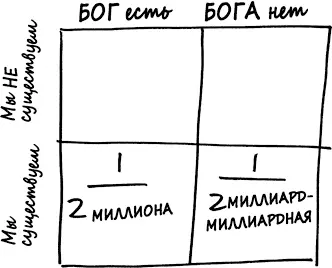
На этом этапе мы можем проанализировать эмпирические данные, а именно что мы существуем. Следовательно, истина находится где-то в нижней строке матрицы. А в нижней строке вы отчетливо видите, что вероятность в клетке «Бог есть» гораздо больше (в триллион раз!) вероятности в клетке «Бога нет».

По существу, это и есть выдвинутый Пейли «аргумент о замысле», как сказал бы современный приверженец байесовской теории. Существует много возражений против этого аргумента о замысле, а также огромное множество агрессивных книг на тему «вы должны стать такими же убежденными атеистами, как я», в которых можно прочитать об этих возражениях, поэтому позвольте мне сосредоточить свое внимание на возражении, которое ближе всего к рассматриваемым математическим концепциям. Речь идет о возражении «самый чистый человек в университете».

Вам наверняка известно, что самым знаменитым изречением Шерлока Холмса после восклицания «Элементарно, Ватсон!» было объяснение логического вывода: «Мой старый принцип состоит в том, чтобы исключить все невозможное. То, что останется, каким бы невероятным это ни выглядело, должно быть истиной».

Разве это не звучит невозмутимо, разумно и неоспоримо?

Но это еще не все. Шерлоку Холмсу следовало бы сказать нечто в таком роде:

Мой старый принцип состоит в том, чтобы исключить все невозможное. То, что останется, каким бы невероятным это ни выглядело, должно быть истиной, если только эта истина не является гипотезой, которую вам не пришло в голову проанализировать.

Менее лаконично, зато более корректно. Люди, которые пришли к выводу о том, что мой друг – самый нечистоплотный человек в университете, рассматривали только две гипотезы:

Чистюля: мой друг меняет футболки, стирает их, а затем снова начинает их менять, как нормальный человек.

Грязнуля: мой друг – нечистоплотный дикарь, который носит грязную одежду.

Вы можете начать с какой-либо априорной вероятности; исходя из своих воспоминаний об учебе в университете, я могу предположить, что было бы правильным присвоить теории Грязнули вероятность 10 %. Но на самом деле не имеет значения, какую априорную вероятность вы выберете: теорию Чистюли опровергает наблюдение, что мой друг носит одну и ту же футболку каждый день. «Если исключить невозможное…»

Но подождите-ка, мистер Холмс: истинное объяснение, Ленивый предприниматель – это гипотеза, не вошедшая в список.

Аргумент о замысле сопряжен с такой же проблемой. Если вы допускаете только две гипотезы: БОГА НЕТ и БОГ ЕСТЬ, – богатую структуру живого мира вполне можно использовать в качестве доказательства в пользу истинности второй, а не первой гипотезы.

Однако есть и другие возможности. Как насчет гипотезы БОГИ ЕСТЬ, согласно которой мир в спешке был создан группой богов, пререкающихся друг с другом? В это верили многие великие цивилизации. Кроме того, вы ведь не можете отрицать, что существуют такие аспекты мира природы (здесь мне в голову приходит бамбуковый медведь), которые кажутся скорее результатом неохотного бюрократического компромисса, а не творением разума всеведущего божества, осуществляющего полный контроль над процессом творения. Если мы начнем с присвоения одной и той же априорной вероятности гипотезам БОГ ЕСТЬ и БОГИ ЕСТЬ – а почему бы и нет, если мы следуем принципу безразличия? – тогда байесовский вывод должен привести нас к гораздо большей уверенности в истинности не теории БОГ ЕСТЬ, а теории БОГИ ЕСТЬ [160].

Но зачем останавливаться на этом? Историям о происхождении Вселенной нет конца. Еще одна теория, которой придерживаются некоторые приверженцы имитационного моделирования, гласит, что на самом деле мы вообще не люди, а модели, существующие на суперкомпьютере, созданном другими людьми [161]. Это звучит нелепо, но многие люди весьма серьезно относятся к этой идее (самый известный из них профессор философии Оксфордского университета Ник Бостром {153}), а с точки зрения байесовской теории трудно объяснить, почему должно быть иначе. Людям нравится строить модели, имитирующие события реального мира; безусловно, если человечество не прекратит свое существование, наша способность создавать такие модели будет только усиливаться. В связи с этим вполне можно представить, что в свое время одним из элементов данных моделей станут обладающие сознанием существа, которые считают себя людьми.