Джордан Элленберг - Как не ошибаться. Сила математического мышления

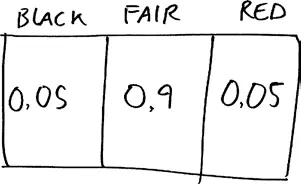
В этой матрице записано то, что в теории вероятностей обозначается термином «априорная вероятность». Разные люди по-разному оценивают значения априорной вероятности: настоящий циник мог бы приписать каждой теории вероятность 1/3, тогда как человек с твердой верой в высокую нравственность производителей колес рулетки может приписать теориям red и black вероятность всего 1 % в случае каждой из них.

Однако эти априорные вероятности не являются фиксированными. Если мы получим данные, говорящие в пользу той или иной теории (скажем, шарик пять раз подряд выпадает на красное), степень нашей уверенности в истинности различных теорий может измениться. Как это могло бы проявиться в данном случае? Лучший способ выяснить это сводится к тому, чтобы рассчитать больше условных вероятностей и нарисовать матрицу большего размера.

Какова вероятность, что мы запустим колесо рулетки пять раз и получим последовательность RRRRR? Ответ зависит от того, какая теория истинна. В случае теории fair при каждом запуске колеса рулетки вероятность того, что шарик попадет в красную ячейку, равна 1/2, а значит, вероятность получения последовательности RRRRR составляет

1/2 × 1/2 × 1/2 × 1/2 × 1/2 = 1/32 = 3,125 %.

Другими словами, вероятность последовательности RRRRR точно такая же, как и в случае остальных 31 последовательности.

Однако, если верна теория BLACK, вероятность попадания шарика в красную ячейку при каждом запуске равна 40 %, или 0,4, а значит, вероятность последовательности RRRRR составляет:

0,4 × 0,4 × 0,4 × 0,4 × 0,4 = 1,024 %.

Если же верна теория red, вероятность попадания шарика в красную ячейку при каждом запуске равна 60 %, а значит, вероятность последовательности RRRRR составляет:

0,6 × 0,6 × 0,6 × 0,6 × 0,6 = 7,76 %.

Теперь давайте увеличим количество клеток в матрице с трех до шести.

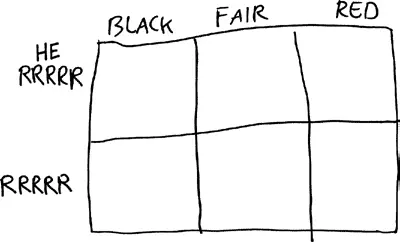
Столбцы этой матрицы по-прежнему соответствуют трем теориям: black, fair и red. Но теперь мы разбиваем каждый столбец на две клетки, одна из которых соответствует получению последовательности RRRRR, а другая – отсутствию этой последовательности. Мы уже выполнили все математические вычисления, необходимые для определения чисел, которые необходимо записать в клетках матрицы. Например, априорная вероятность того, что fair – это правильная теория, составляет 0,9. А 3,125 % от этой вероятности, 0,9 × 0,03125 (или около 0,0281), следует записать в клетке, в которой fair – правильная теория, а шарики выпадают в последовательности RRRRR. Число 0,8719 попадает в клетку «теория fair истинна, не RRRRR», так что сумма вероятностей в столбце fair составляет 0,9.

Априорная вероятность попадания в столбец red равна 0,05. Следовательно, вероятность того, что теория red истинна и что шарики выпадают в последовательности RRRRR, составляет 7,76 % от 5 %, или 0,0039. Это составляет 0,0461 для клетки «теория red истинна, RRRRR».

Теория black также имеет априорную вероятность 0,05. Однако эта теория не так хорошо согласуется с вероятностью последовательности RRRRR. Вероятность того, что теория black истинна, а шарики выпадают в последовательности RRRRR, равна всего 1,024 % от 5 %, или 0,0005.

Вот как выглядит наша матрица с заполненными клетками.

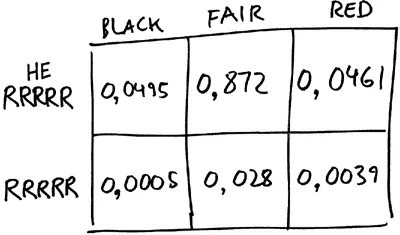
(Обратите внимание, что сумма чисел во всех клетках матрицы равна единице. Именно так и должно быть, поскольку шесть клеток матрицы представляют все возможные варианты.)

Что произойдет с нашими теориями, если мы запустим колесо и действительно получим последовательность RRRRR? Это была бы хорошая новость для теории red и плохая новость для теории black. Именно это мы и видим. Попадание шарика в красные ячейки пять раз подряд означает, что мы находимся в нижней строке матрицы из шести клеток, причем вероятность 0,0005 соответствует теории black, 0,028 теории fair и 0,0039 теории red. Другими словами, при условии формирования последовательности RRRRR наша новая оценка состоит в том, что вероятность истинности теории fair в семь раз больше вероятности теории red, а вероятность теории red примерно в восемь раз больше вероятности теории black.

Если вы хотите перевести эти относительные величины в вероятность, выраженную в процентах, вам нужно просто вспомнить, что общая вероятность всех возможных вариантов должна быть равной единице. Сумма чисел в нижней строке равна 0,0325; следовательно, чтобы обеспечить сумму этих чисел, равную единице, без изменения соотношения между ними, можно просто разделить каждое число на 0,0325. В итоге вы получите следующее.