Джордан Элленберг - Как не ошибаться. Сила математического мышления

На самом деле Гальтон сделал еще кое-что: он тщательно начертил на своей диаграмме разброса кривые линии, вдоль которых плотность точек была примерно одинаковой. Подобные кривые называются «изоплеты» – и вам они известны, разве что не под таким именем. Если мы возьмем карту США и проведем на ней линию, соединяющую места, в которых сегодня температура 25 градусов, 10 градусов или любая другая фиксированная температура, получатся знакомые кривые синоптической карты, которые называются «изотермы». Настоящая синоптическая карта содержит также «изобары», соединяющие места с одинаковым атмосферным давлением, или «изонефы», соединяющие места с одинаковым облачным покровом. Если измерять высоту, а не температуру, то изоплеты представляют собой контурные линии, называющиеся «изогипсы», которые можно найти на топографических картах. Представленная ниже карта изоплет показывает среднегодовое количество снежных бурь на континентальной части территории США {221}:

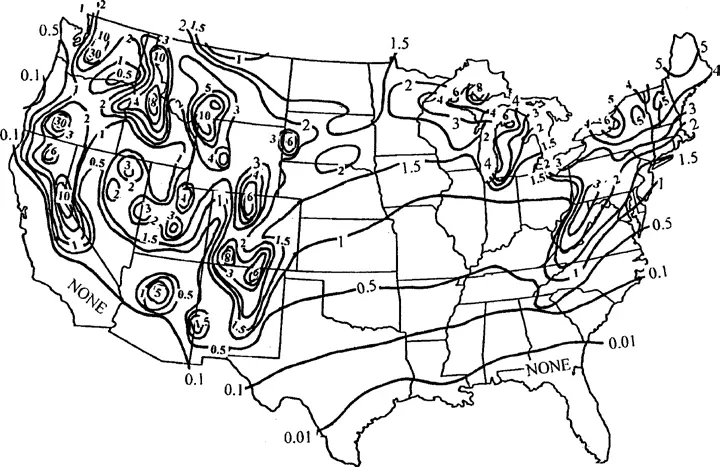
Изоплету изобрел не Гальтон. Первую опубликованную карту изоплет создал в 1701 году Эдмунд Галлей, британский Королевский астроном, который объяснял королю, как правильно оценивать аннуитеты [262]. Навигаторы уже знали, что магнитный северный меридиан не всегда совпадает с истинным северным меридианом. Понимание того, где и в какой степени они не совпадают, играло важнейшую роль для успешных путешествий по океану. Кривые на карте Галлея, получившие название «изогоны», показывали мореплавателям области одинаковых расхождений между магнитным и истинным северным меридианом {222}. Эти данные были основаны на измерениях, сделанных Галлеем на борту корабля Paramore, который несколько раз пересекал Атлантический океан во главе с Галлеем. (Этот человек знал, чем себя занять между визитами комет.)

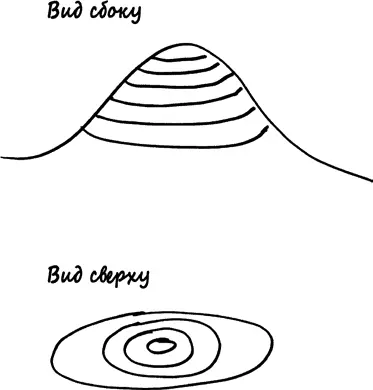
Гальтон обнаружил поразительную регулярность: все его изоплеты представляли собой эллипсы, каждый из которых был заключен в следующий, причем у всех эллипсов был один центр. Это напоминало контурную карту горы идеальной эллиптической формы с вершиной, которой соответствовали два значения роста, чаще всего встречавшиеся в выборке Гальтона: средний рост родителей и детей. Эта гора представляет собой не что иное, как трехмерную версию колоколообразной кривой под названием «шлем жандарма», которую изучал Абрахам де Муавр; сегодня мы используем термин «двумерное нормальное распределение».

Когда рост сыновей совершенно не зависит от роста родителей (как на второй диаграмме разброса), эллипсы Гальтона представляют собой круги, данные на диаграмме также образуют круг. Когда рост сыновей полностью зависит от наследственности, а элемент случайности отсутствует (как на первой диаграмме разброса), данные расположены вдоль прямой линии, что можно представить себе как самый вытянутый эллипс. Между этими двумя крайними случаями мы имеем эллипсы различной толщины, которую специалисты по классической геометрии называют «эксцентриситетом» эллипса. Эксцентриситет отображает степень, в которой рост отца определяет рост сына. Высокий эксцентриситет означает, что имеет место сильная наследственность и слабая регрессия к среднему значению; низкий эксцентриситет означает противоположное: ситуацию контролирует регрессия к среднему. Гальтон называл этот показатель «корреляцией» – мы используем его до сих пор. Если эллипс Гальтона почти круглый, корреляция близка к 0; если эллипс сильно вытянут в направлении с северо-востока на юго-запад, корреляция близка к 1. С помощью эксцентриситета (геометрической величины, возраст которой совпадает с возрастом работы Аполлония Пергского в III столетии до нашей эры). Гальтон нашел способ измерять связь между двумя переменными и благодаря этому решил важнейшую задачу биологии XIX столетия: задачу количественного анализа наследственности.

Возможно, здоровый скептицизм заставляет вас задать вопрос: что если данные на диаграмме разброса не образуют эллипс? Что тогда? На этот вопрос есть прагматический ответ: на практике диаграммы разброса реальных массивов данных во многих случаях действительно образуют фигуры, близкие к эллипсам, – не всегда, но достаточно часто, чтобы сделать этот метод широко применимым. Вот как выглядит диаграмма разброса, если отобразить на ней долю избирателей, проголосовавших за Джона Керри в 2004 году, в сравнении с долей избирателей, проголосовавших за Барака Обаму в 2008 году. Каждая точка соответствует одному избирательному округу.