Джордан Элленберг - Как не ошибаться. Сила математического мышления

Диаграмма «петушиный гребень» и диаграмма разброса согласуются с нашими когнитивными способностями: мозг человека плохо воспринимает столбцы чисел, но прекрасно справляется с анализом закономерностей и данных, представленных в двумерном поле зрения.

В некоторых случаях это не вызывает никаких трудностей. Предположим, например, что каждый сын и отец имеют одинаковый рост, как у меня с моим отцом. Это та самая ситуация, когда случай не играет никакой роли [260], а ваш рост целиком и полностью зависит от унаследованных от отца качеств. В таком случае все точки нашей диаграммы разброса будут иметь одинаковые координаты x и y ; другими словами, они будут сосредоточены в непосредственной близости от диагональной линии, уравнение которой x = y :

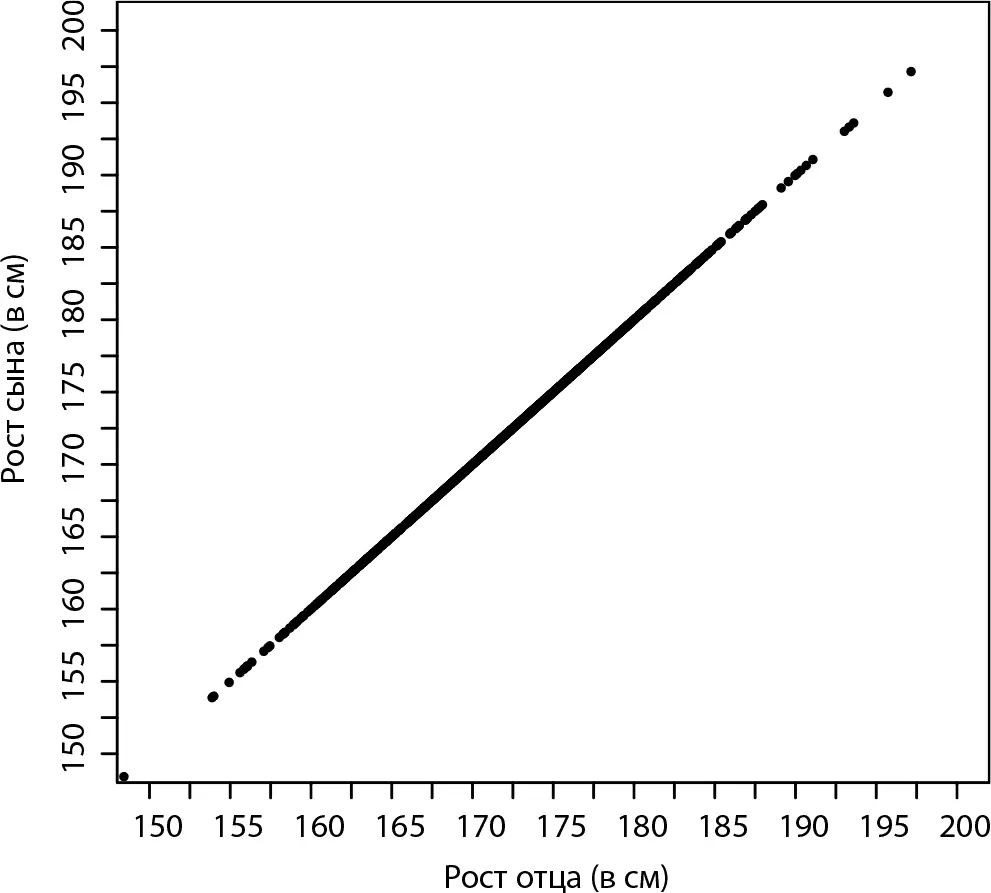
Обратите внимание, что плотность точек больше у середины и меньше у концов графика; это означает, что количество мужчин ростом 176 сантиметров больше количества мужчин ростом 185 сантиметров и 163 сантиметра.

Что происходит в противоположном случае, когда рост сыновей никак не связан с ростом отцов? При таком варианте диаграмма разброса выглядела бы так:

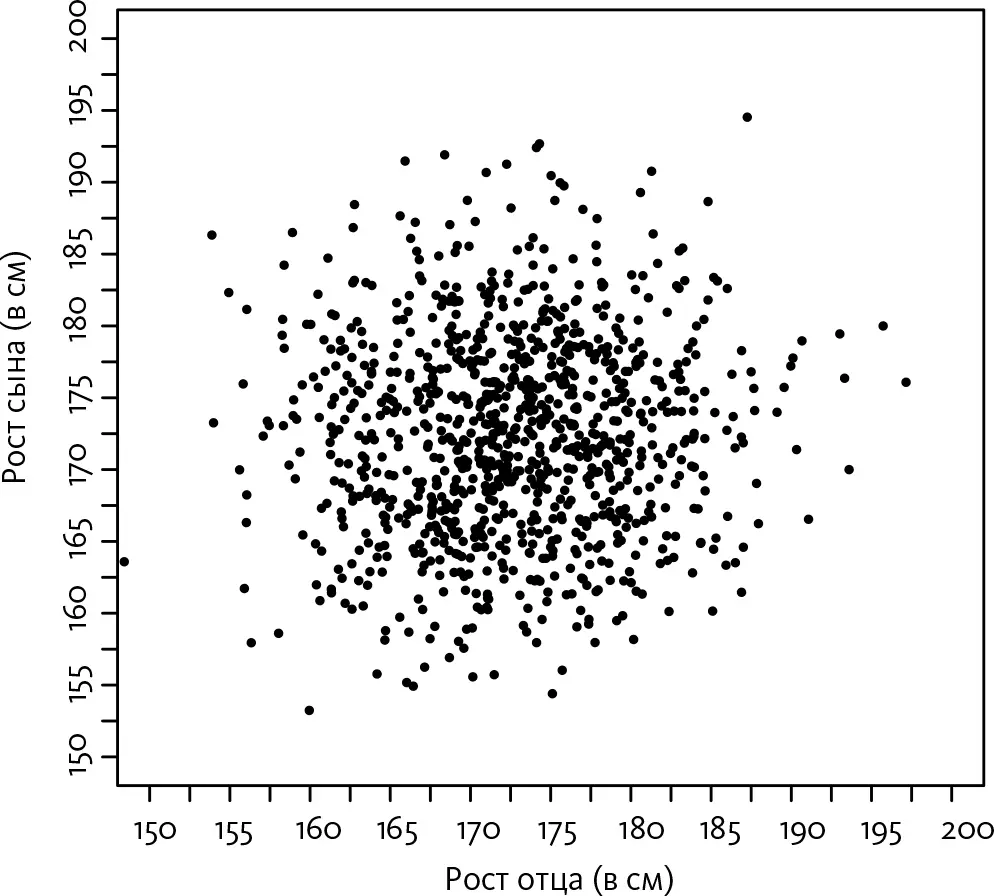
На этом рисунке, в отличие от предыдущего, нет смещения точек в сторону диагонали. Если вы обратите внимание только на сыновей, у отцов которых рост 185 сантиметров (вертикальный срез в правой части диаграммы разброса), точки, соответствующие росту сыновей, по-прежнему сосредоточены в области 176 сантиметров. Будем говорить, что условное математическое ожидание роста сына (другими словами, каким в среднем будет рост сына при условии, что у отца рост 185 сантиметров) совпадает с безусловным математическим ожиданием (средний рост сыновей, рассчитанный без учета роста отца). Именно так выглядела бы диаграмма Гальтона, если не было бы наследственных особенностей, оказывающих влияние на рост. Это регрессия к среднему значению в самом выраженном виде: сыновья высоких отцов возвращаются к среднему росту, оказываясь в итоге не выше сыновей низкорослых отцов.

Однако диаграмма разброса Гальтона не похожа ни на один из этих крайних случаев. Напротив, она представляет собой нечто среднее между ними:

Что представляет собой на этом графике средний рост сына отца, рост которого 185 сантиметров? Я нарисовал вертикальный срез, чтобы показать, какие точки на диаграмме разброса соответствуют этим парам «отец – сын».

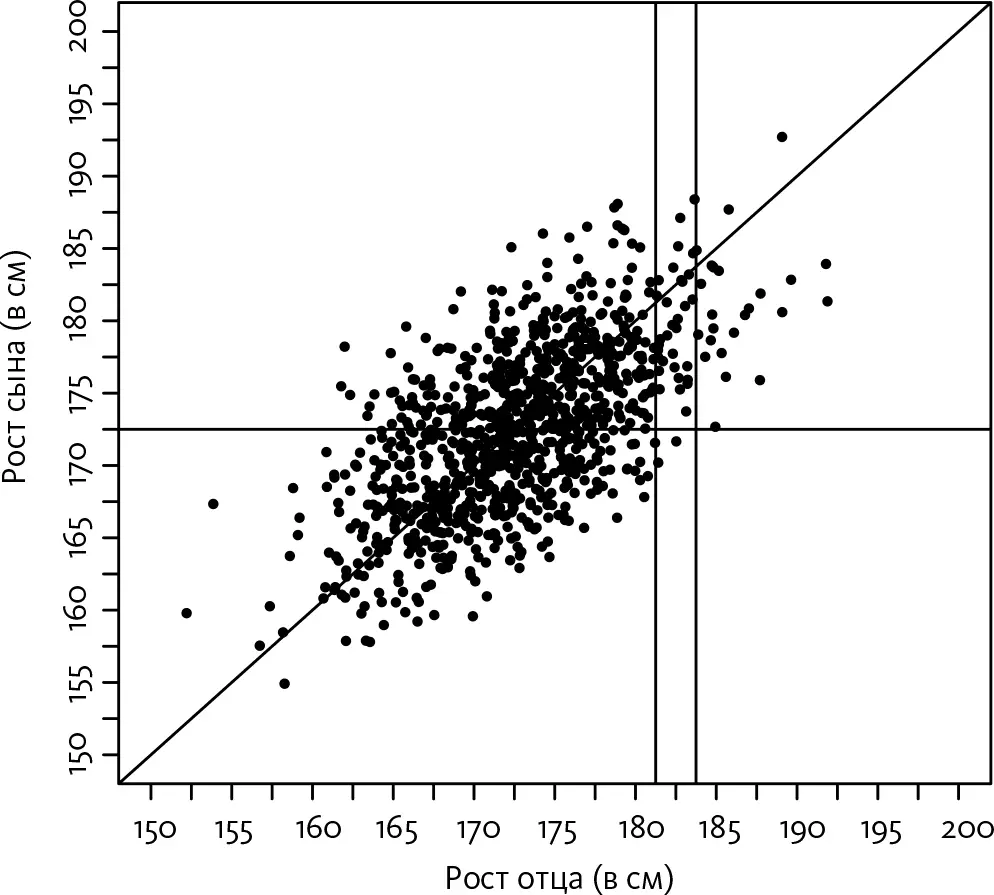
Как видите, в срезе «отец ростом 185 сантиметров» концентрация точек под диагональю больше, чем над ней, а значит, сыновья в среднем ниже ростом, чем их отцы. С другой стороны, они явно выше 175 сантиметров, роста обычного мужчины. В массиве данных, которые я отобразил на этом графике, средний рост этих сыновей составляет около 183 сантиметров, то есть они выше среднего роста, но не такие высокие, как отцы. Вы смотрите сейчас на изображение регрессии к среднему значению.

Гальтон сразу заметил, что его диаграммы разброса, полученные как результат взаимодействия между наследственностью и случаем, имеют далеко не случайную геометрическую структуру. Создавалось впечатление, что все они в той или иной мере заключены в эллипс с центром в точке, в которой отцы и дети имеют одинаковый средний рост.

Эту наклонную эллиптическую форму можно обнаружить даже в первичных данных, представленных в таблице из работы Гальтона «Регрессия к посредственности на примере наследуемого роста», опубликованной в 1886 году: обратите внимание на фигуру, которую образуют отличные от нуля числа в этой таблице. Кроме того, из таблицы становится ясно, что я не все рассказал о совокупности данных Гальтона. В частности, его ось y – это не «рост отца», а «среднее между ростом отца и ростом матери, умноженном на 1,08» [261](что Гальтон называет «средним родителем»).

Примечание. При расчете медиан учитывались средние значения показателей в соответствующих клетках таблицы. В заголовках столбцов указаны числа 62,2, 63,2 и т. д., поскольку данные наблюдений неравномерно распределены между показателями 62 и 63, 63 и 64 и т. д. с сильным смещением в сторону целых дюймов. Тщательно все взвесив, я пришел к выводу, что заголовки столбцов в предложенном виде лучше всего удовлетворяют заданным условиям. В случае роста средних родителей такая неравномерность не была очевидной.