Джордан Элленберг - Как не ошибаться. Сила математического мышления

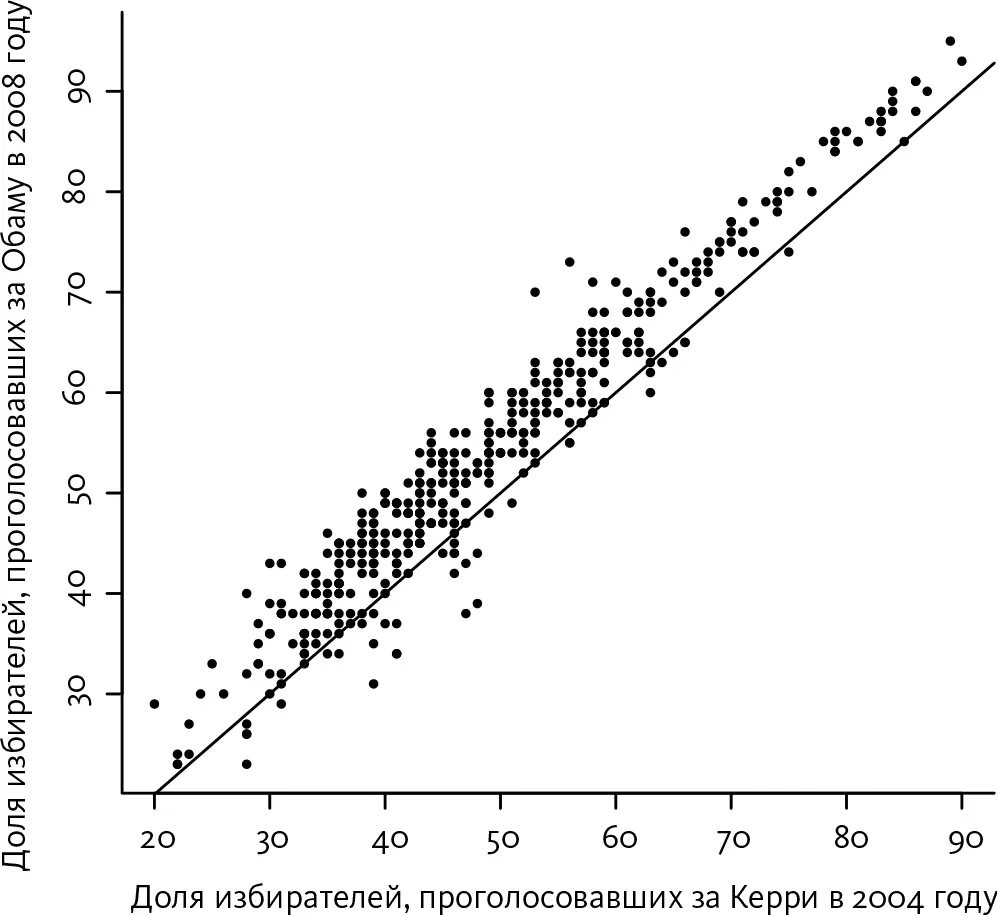
Эллипс здесь налицо, причем очень вытянутый, а это значит, что существует высокая степень корреляции между долей избирателей, проголосовавших за Керри, и долей избирателей, проголосовавших за Обаму. Очевидно, что б о льшая часть графика расположена над диагональю; это говорит о том, что в целом Обама получил больше голосов, чем Керри.

На следующем графике представлены данные о ежедневных изменениях курсов акций Google и General Electric (GE) за несколько лет.

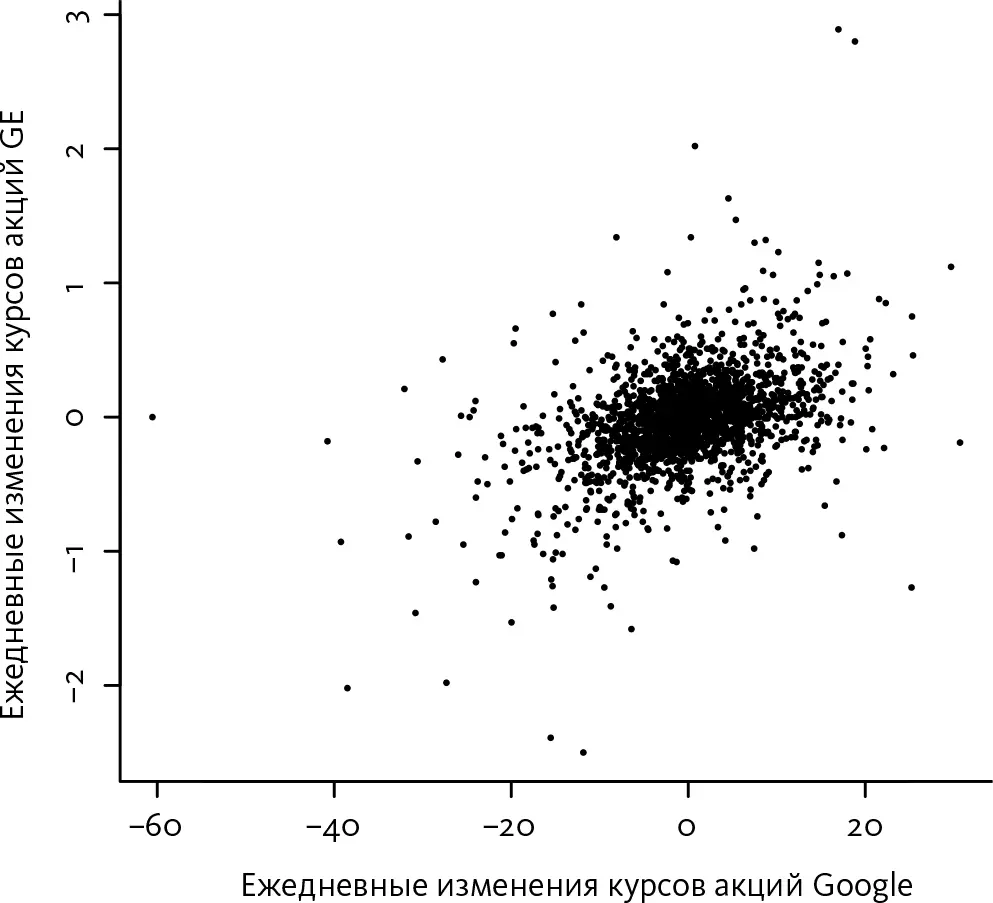
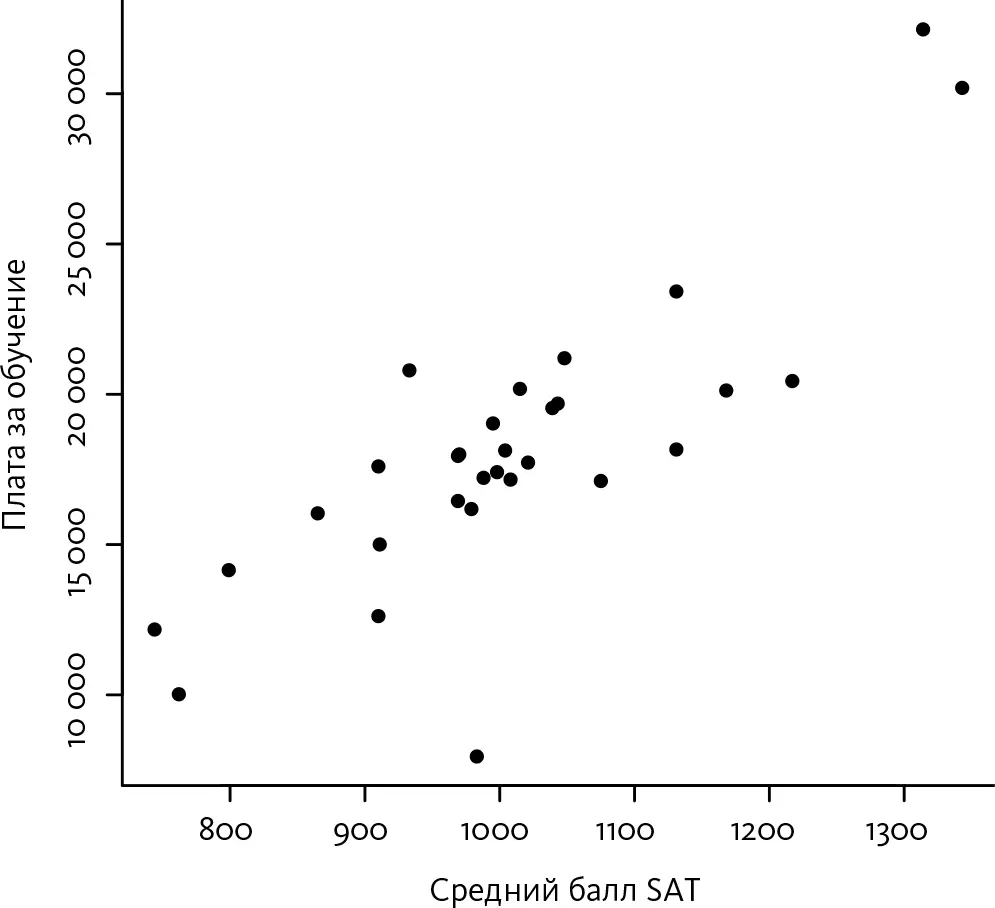
Следующим будет рисунок, который мы уже видели, – график взаимозависимости между стоимостью обучения в нескольких университетах штата Северная Каролина и средним баллом SAT.

Далее представлены 50 штатов США, расположенные на диаграмме разброса по среднему доходу и доле избирателей, проголосовавших за Джорджа Буша во время президентских выборов 2004 года {223}. На этой диаграмме богатые либеральные штаты, такие как Коннектикут, расположены в нижней правой части диаграммы, а поддерживающие республиканцев штаты с более скромными доходами, такие как Айдахо, – в верхней левой части.

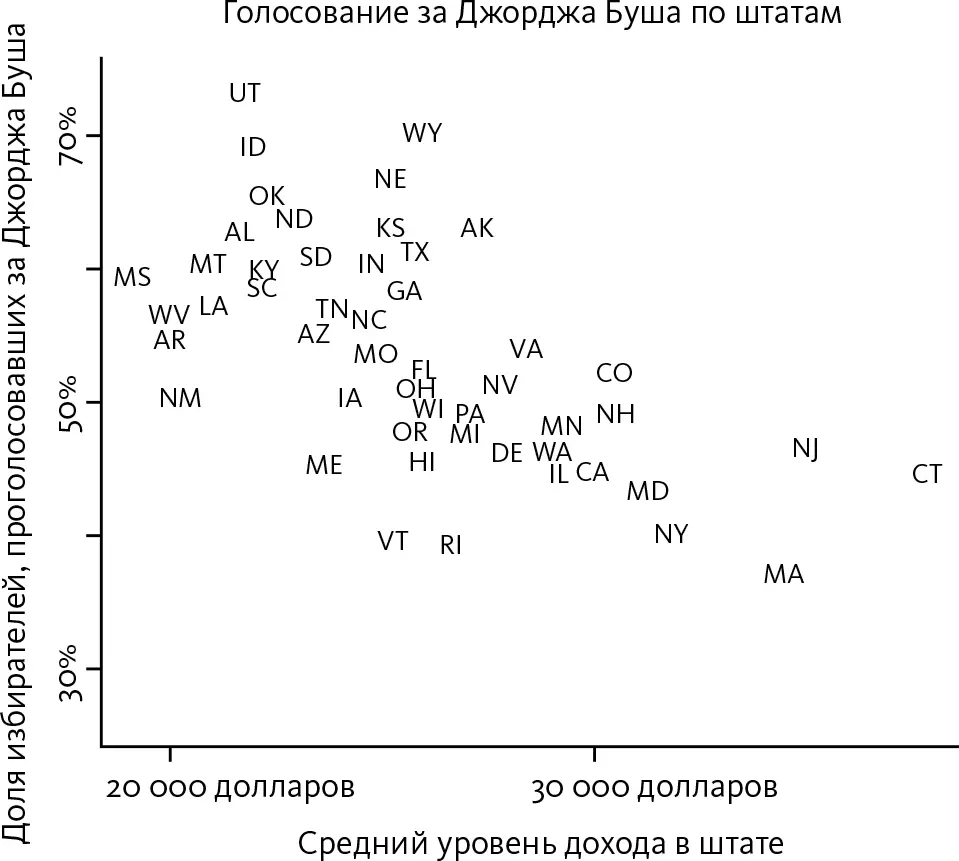
Эти данные взяты из самых разных источников, однако все четыре диаграммы разброса имеют примерно такую же эллиптическую форму, что и диаграмма роста родителей и детей. В первых трех случаях имеет место положительная корреляция: увеличение одной переменной связано с увеличением другой; при этом эллипс вытянут с северо-востока на юго-запад. На последнем графике отображена отрицательная корреляция: в целом более богатые штаты больше поддерживают демократов, а эллипс вытянут с северо-запада на юго-восток.

Аполлоний и древнегреческие геометры представляли себе эллипсы как конические сечения – поверхности, полученные пересечением конуса плоскостью. Кеплер показал (хотя астрономическому сообществу понадобилось несколько десятилетий, чтобы понять это), что планеты движутся по эллиптическим орбитам, а не по круговым, как считалось ранее. Теперь та же кривая возникает в качестве естественной фигуры, к которой заключены данные о росте родителей и детей. Чем это можно объяснить? Причина не в том, что существует некий невидимый конус, управляющий наследственностью, который в случае отсечения под правильным углом дает эллипсы Гальтона. Причина также не в том, что некая форма генетического притяжения приводит к появлению эллиптических фигур на диаграммах Гальтона посредством ньютоновских законов механики.

Причина заключается в одном фундаментальном свойстве математики – в каком-то смысле именно это свойство сделало математику столь полезной для естествоиспытателей. В математике существует множество сложных объектов, но совсем немного простых. Следовательно, если у вас есть задача, решение которой допускает простое математическое описание, значит, существует только несколько вариантов такого решения . Таким образом, самые простые математические объекты широко распространены и выполняют множество обязанностей в качестве решений научных задач разных типов.

Самые простые линии – прямые. Очевидно, что прямые линии присутствуют в природе повсюду, от граней кристаллов до траектории движущихся тел при отсутствии силы, которая на них воздействует. Следующий тип простейших линий – линии, представленные квадратными уравнениями [263], то есть уравнениями, в которых друг на друга умножаются не более двух переменных. Таким образом, возведение переменной в квадрат, или умножение двух разных переменных, разрешено, тогда как возведение переменной в куб, или умножение одной переменной на квадрат другой, строго запрещено. Линии этой категории, в том числе эллипсы, из уважения к истории называют коническими сечениями, однако более прогрессивные специалисты по алгебраической геометрии называют их квадриками [264], или кривыми второго порядка . Существует множество квадратных уравнений, причем любое из них имеет такой вид: