Джордан Элленберг - Как не ошибаться. Сила математического мышления

Похоже на полную чушь. И так оно и есть! Однако, когда математика говорит, что нечто похоже на чушь, математики не уходят прочь, пожав плечами. Мы начинаем искать тот поворот, после которого либо математика, либо наша интуиция пошла не по тому пути [197]. Эту головоломку, известную как санкт-петербургский парадокс , впервые сформулировал Николай Бернулли (двоюродный брат Даниила) примерно на тридцать лет раньше, и многие специалисты по теории вероятностей того времени ломали над ней голову, но так и не пришли к удовлетворительному выводу. Младший Бернулли предложил замечательный способ разрешения этого парадокса – важнейший результат, с тех пор лежащий в основе экономического мышления по поводу неопределенной ценности. Бернулли утверждал: было бы ошибкой говорить, что дукат – это просто дукат. Дукат в руках богатого человека имеет иную ценность, чем дукат в руках крестьянина, что можно увидеть даже по тому, насколько по-разному эти двое относятся к своим деньгам. В частности, две тысячи дукатов – это не в два раза лучше одной тысячи, поскольку для человека, у которого уже есть тысяча дукатов, тысяча дукатов имеет меньшую ценность, чем для человека, у которого нет ничего. В два раза больше дукатов не означает в два раза больше ютилей: не все линии прямые, а зависимость между деньгами и их полезностью отображается в виде одной из таких непрямых линий.

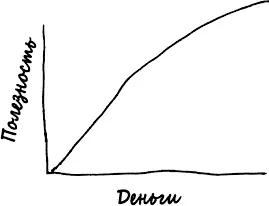
Бернулли считал, что такая полезность возрастает по логарифмическому закону, то есть k -й приз в размере 2k дукатов имеет ценность всего k ютилей. Помните: мы можем представить логарифм как своего рода совокупность цифр, а значит, если сформулировать гипотезу Бернулли в долларах, то она гласит, что богатые люди измеряют ценность своих денег в количестве цифр после долларового знака: миллиардер настолько богаче миллионера с капиталом 100 миллионов долларов, насколько миллионер с капиталом 100 миллионов долларов богаче миллионера с капиталом 10 миллионов долларов.

В формулировке Бернулли ожидаемая полезность петербургской игры представляет собой сумму:

(1/2) × 1 + (1/4) × 2 + (1/8) × 3 + (1/16) × 4 +…

Это укрощает парадокс, поскольку, оказывается, эта сумма больше не является бесконечной или даже большой. На самом деле существует замечательный прием, который позволяет нам точно вычислить эту сумму:

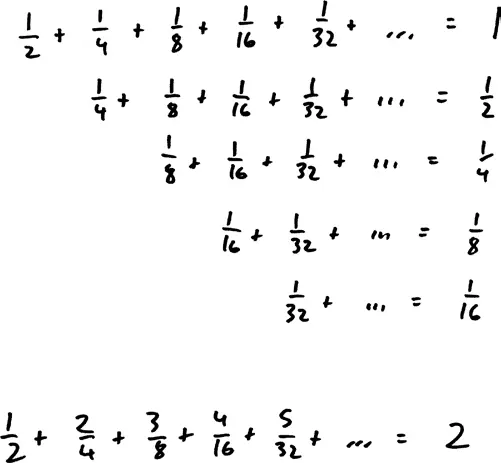
Сумма первого ряда, (1/2) + (1/4) + (1/8) + …, равна 1; это тот самый бесконечный ряд, который обнаружил Зенон в главе 2. Второй ряд такой же, как и первый, только каждый его член разделен на 2, а значит, сумма этого ряда должна быть равной половине суммы первого ряда, то есть 1/2. Точно так же третий ряд, представляющий собой второй ряд, в которой каждый член разделен на 2, должен быть равным половине суммы второго ряда, то есть 1/4. Сумма всех чисел, представленных в правой части этого треугольника, равна 1 + 1/2 + 1/4 + 1/8 + …, на единицу больше, чем сумма ряда Зенона, другими словами, 2.

Но что если мы просуммируем сначала столбцы, а не ряды? Как и в случае с отверстиями в боковой панели стереосистемы моих родителей, не имеет значения, как считать – по горизонтали или по вертикали: сумма останется одной и той же [198]. В первом столбце есть только число 1/2; во втором два числа 1/4, то есть (1/4) × 2; в третьем три числа 1/8, то есть (1/8) × 3, и так далее. Ряд, сформированный из сумм столбцов, – это не что иное, как сумма, которую установил Бернулли для изучения санкт-петербургской задачи. А эта сумма представляет собой сумму всех чисел бесконечного треугольника, то есть 2. Следовательно, сумма денег, которую должен заплатить Павел, равна такому количеству дукатов, которое, согласно его личной кривой полезности, стоит 2 ютиля [199].

Помимо того факта, что кривая полезности изгибается вниз по мере увеличения количества денег, ее форму невозможно определить точно [200], хотя современные экономисты и психологи постоянно изобретают все более замысловатые эксперименты, призванные внести ясность в наше понимание свойств этой кривой. («А теперь, если не возражаете, удобно положите голову в центре камеры функционального магнитно-резонансного томографа, и я попрошу вас упорядочить следующие шесть покерных стратегий, от самых привлекательных до наименее привлекательных. Затем, если вы не против, полежите спокойно еще немного, пока мой ассистент возьмет у вас мазок из ротовой полости…»)