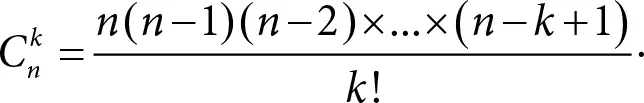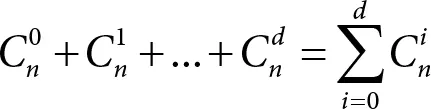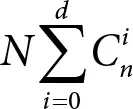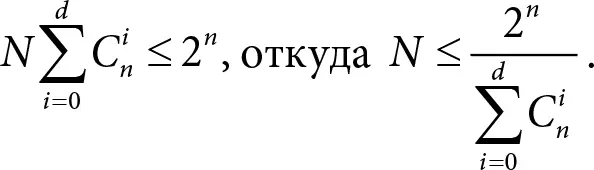Андрей Райгородский - Кому нужна математика? Понятная книга о том, как устроен цифровой мир

Допустим, нам нужно послать землекопов на объекты и мы хотим минимизировать стоимость работ. Для начала мы берем совершенно произвольное расписание и получаем стоимость работ, скажем 50 000 рублей. Это наш максимум, и мы постараемся его уменьшить.

Теперь запускаем симплекс-метод и получаем дробное решение. Например, на объект А нужно отправить 2 и 2/3 землекопа. Допустим, общая стоимость работ при этом составит 40 000 рублей. Это пока не дает нам плана работ, потому что решение не в целых числах. Зато мы знаем, что это решение оптимальное, то есть при любом другом (в том числе целочисленном) решении стоимость получится никак не меньше 40 000 рублей. Значит, наша стоимость в результате будет между 40 000 и 50 000 рублей.

Дальше начинаем «разветвлять» решение. У нас есть два варианта: A ≤ 2 и A ≥ 3. Для каждого из них мы снова решаем задачу линейного программирования. Допустим, стоимость получилась 43 000 рублей при A ≥ 3 и 51 000 при A ≤ 2. Отсекаем вариант A ≤ 2, поскольку у нас уже есть более выгодное решение. В результате делаем вывод, что A ≥ 3, а минимальная стоимость теперь 43 000 рублей. Если при этом все переменные получились целочисленные, то мы нашли решение. А если у нас еще остались дробные переменные, то каждую из них разветвляем снова. И так до тех пор, пока не найдем решения в целых числах.

Назад к Главе 2

Для начала рассмотрим последовательности длины 5. Сколькими способами мы можем выбрать первый элемент последовательности? Очевидно, что вариантов 2: ноль или единица. Теперь давайте посмотрим на второй элемент. Для него у нас тоже есть два варианта, причем при любом выборе первого элемента последовательности. Значит, число способов выставить друг за другом первые два элемента равно четырем. Точно так же для каждого из этих четырех вариантов есть два способа выбрать третий элемент последовательности и так далее. В итоге для кодового слова длины 5 получаем

2 × 2 × 2 × 2 × 2 = 2 5= 32.

Аналогично число разных последовательностей длины 4 равно 2 4= 16, а число разных последовательностей длины 8 равно 2 8= 256. Для любой заданной длины n получаем 2 n разных последовательностей из нулей и единиц.

Допустим, мы пользуемся словами длиной n и наш код состоит из N таких слов.

Если код исправляет d ошибок, то шары Хэмминга с центрами в кодовых словах и радиусами d попарно не пересекаются. Объем шара (то есть количество слов в нем) нетрудно вычислить. Сколько слов отстают от центра шара на заданное расстояние k ? Разумеется, столько, сколькими способами можно выбрать те k позиций из n возможных, в которых произойдут помехи. Это число способов называется числом сочетаний из п по k и обозначается C k n . Для того чтобы его записать, нам понадобятся произведения вида

k × ( k − 1) × … × 2 × 1.

Такое произведение принято обозначать записью

k !

и она читается как k факториал. Легко увидеть, что, конечно, 1! = 1, и принято считать, что 0! = 1. Заметим, что факториал уже встречался нам в главе 2 в разделе «Проклятие размерности». Там мы показали, что факториал растет очень быстро. Например, 25! – это колоссальное число.

Число сочетаний вычисляется по формуле

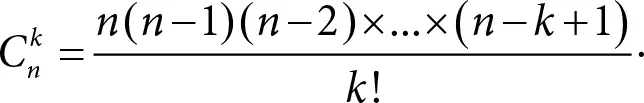
Мы приводим вывод этой известной формулы ниже, в приложении 3. Легко проверить, скажем, что C¹ n , и действительно мы можем выбрать одну позицию из n ровно n способами.

Значит, всего внутри шара

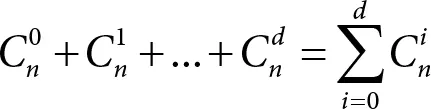
слов. Здесь слагаемое C 0 n =1 – это число слов, отстоящих от центра на расстояние 0. Такое слово только одно – сам центр. Поскольку шары с центрами в кодовых словах попарно не пересекаются, то всего в них находится

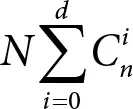
различных слов. Но это количество заведомо не превосходит числа всех возможных кодовых слов, которое, как мы уже знаем, равно 2n . Таким образом,

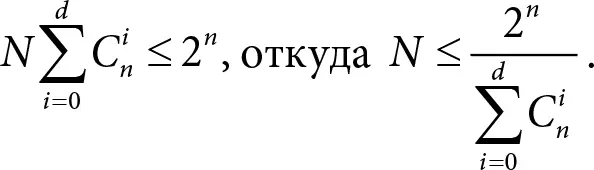
Эта формула и есть граница Хэмминга. В нашем примере, когда n = 10, d = 2, получаем