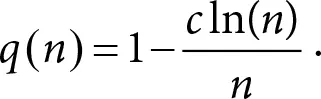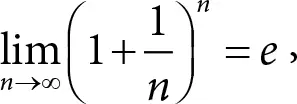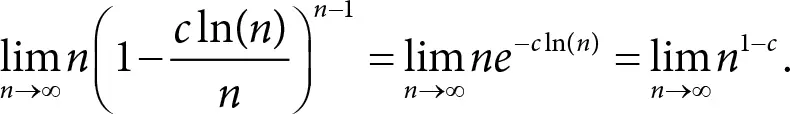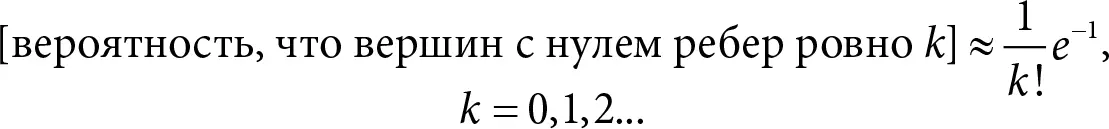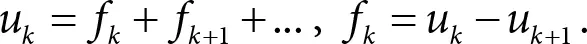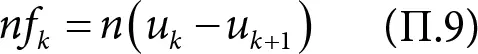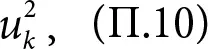Андрей Райгородский - Кому нужна математика? Понятная книга о том, как устроен цифровой мир

( q ( n )) n− 1.

Поскольку всего вершин п, то в среднем число вершин, которые не соединены ребрами ни с одной другой вершиной, составит

n ( q ( n )) n− 1.

Возьмем, как и прежде,

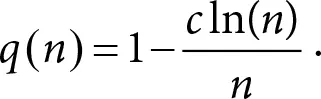
Вспомните один известный замечательный предел

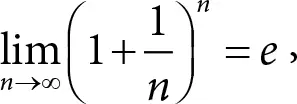
где е – основание натурального логарифма. Интуитивно результат следует из похожего предельного перехода:

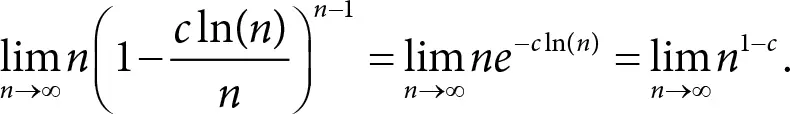
Давайте посмотрим, о чем нам говорит эта формула.

Если c < 1, то в среднем число вершин, у которых нет ни одного ребра, стремится к бесконечности. В этом случае таких вершин будет очень много, связность сети с большой вероятностью будет потеряна.

Если c > 1, то в среднем число вершин, у которых нет ни одного ребра, стремится к нулю. Значит, с большой вероятностью таких вершин не будет и связность сети сохранится.

Таким образом, мы видим, откуда появляется фазовый переход!

Наконец, если c = 1, то в среднем число вершин, у которых нет ни одного ребра, равно единице. Заметим, что единица – это среднее значение, а в реальности таких вершин может быть 0, 1, 2… Можно доказать, что соответствующее распределение вероятности близко к закону Пуассона с параметром 1:

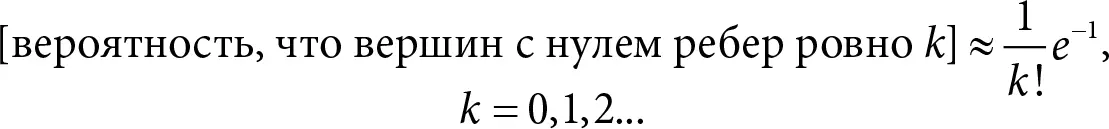
Соответственно, вероятность того, что таких вершин не будет, то есть связность сети сохранится, равна е –1.

Добавим, что это еще не строгое доказательство, потому что мы проанализировали только среднее количество вершин, у которых нет ни одного ребра. Для завершения доказательства нужно еще показать, что в случае c < 1 и c > 1 число вершин без ребер относительно м а ло отклоняется от среднего значения. Для этого разработаны стандартные методы, в частности, основанные на неравенствах Маркова и Чебышева. Эти неравенства названы в честь замечательных русских математиков, стоявших у истоков теории вероятностей.

Назад к Главе 4

Допустим, у нас n серверов. Заявки (или задания) поступают с интенсивностью λ n в единицу времени, и каждый сервер в среднем обрабатывает одно задание в единицу времени, то есть загрузка системы равна λ < 1 (если λ ≥1, то система перегружена, очередь будет расти до бесконечности). Рассмотрим случай, когда n очень велико и стремится к бесконечности.

Обозначим через f k долю серверов, у которых ровно k заявок (заявка, которая находится на обслуживании в данный момент, тоже учитывается). Обозначим через u k долю серверов, у которых заявок k или больше. Значения u k можно легко получить через f k и наоборот:

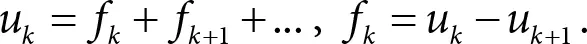
Понятно, что u 0= 1.

Представим, что система находится в равновесии. Тогда у нас в среднем

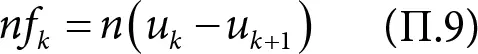
серверов, на которых ровно k заданий. Все эти серверы обрабатывают задания со скоростью одно задание в единицу времени. Другими словами, количество серверов с k заявками или больше уменьшается на n ( u k − u k+1 ) в единицу времени.

Теперь давайте посмотрим, на сколько количество серверов с k заявками или больше увеличивается в единицу времени. Чтобы увеличить число таких серверов, заявки должны поступать на серверы, у которых в данный момент k − 1 заявка. При методе выбора из двух вероятность того, что новое задание попадет на сервер с k или больше заявками, равна

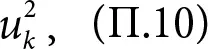
потому что в этом случае оба случайно и независимо выбранных сервера должны иметь k или больше заявок, и для каждого из двух серверов эта вероятность и k [26]. Значит, вероятность того, что новая заявка поступит на сервер, у которого ровно k − 1 заявка, равна