Андрей Райгородский - Кому нужна математика? Понятная книга о том, как устроен цифровой мир

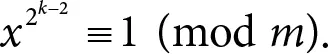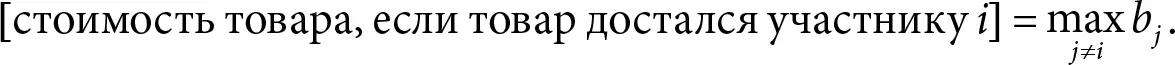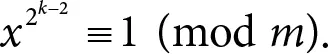
При этом φ (m) = 2 k −1, потому что числа, взаимно простые со степенью двойки, – это все нечетные числа, а их ровно 2 k −1. Значит, для любого х нашлось число

a = 2 k −2< 2 k −1= φ (m) ,

для которого выполняется x a ≡ 1 (mod m ). Получается, что у m = 2 k при k ≥ 3 первообразных корней нет.

Теперь мы можем объяснить, почему в качестве m удобно брать простое число р. Для простого р всегда существуют первообразные корни. На самом деле мы уже говорили о них выше, в приложении 2 к главе 6, только не называли этим термином. Это те самые числа g , которые дают разные остатки от деления на p в (П.15). Например, при p = 3 это g = 2, при p = 5 это g = 2, а при p = 7 это g = 3. В нашем примере в тексте главы число g = 2 – это один из первообразных корней числа p = 19.

Итак, если g – первообразный корень p , то все остатки в (П.15) разные и каждому остатку соответствует единственная степень х (дискретный логарифм, он же индекс), при которой такой остаток получается. Ничего подобного мы не можем сделать, если будем брать остаток от деления на число m , для которого первообразного корня нет. Именно поэтому работают с простыми числами.

Заметим, что первообразные корни есть еще для m = 4, m = p k и m = 2 p k . Но все равно с простыми числами работать проще.

Назад к Главе 6

Хеш-значения – это последовательности из нулей и единиц одинаковой длины. Обозначим длину хеш-значений через т. Тогда получим 2 m разных хеш-значений (см. главу 3и приложение 1к ней).

Теперь допустим, что нам нужно сосчитать n различных объектов. Чтобы присвоить им всем разные хеш-значения, понадобится как минимум n хеш-значений, то есть

Стало быть, m должно быть того же порядка величины, что и log 2( n ).

Алгоритм К-Minimum Values запоминает К самых маленьких хеш-значений длины m , то есть для этого алгоритма нам нужен объем памяти примерно K log 2( n ).

HyperLogLog запоминает только максимальное количество нулей в начале хеш-значений. Если сами хеш-значения длины m , то и нулей может быть не больше, чем т. Значит, нам нужно держать в памяти число между 0 и m . Оно тоже записывается с помощью последовательности нулей и единиц. Какой длины должны быть эти последовательности? Если последовательности длины l , то мы можем записать 2 l разных чисел. Стало быть, чтобы записать m + 1 разных чисел, должно выполняться

В памяти нам нужно держать только l битов информации (последовательность из нулей и единиц длины l ). Из предыдущих формул получается:

Для повышения точности хеш-значения разбивают на r регистров и запоминают максимальное число нулей в каждом регистре отдельно. В результате требуется порядка r log 2(log 2( n )) битов памяти. Относительная точность оценки задается формулой 1,04÷ √ r {36}.

Назад к Главе 7

Рассмотрим аукцион второй цены, на котором один товар разыгрывается между n участниками. Обозначим v i истинную ценность товара для участника i (от английского слова value – ценность). Далее обозначим через b i ставку участника i (от англ. bid – ставка ). Эти обозначения будем использовать для любого i = 1,2, …, n .

Совместимость по стимулам означает, что верна следующая теорема.

Теорема (Викри). Участник i получает максимальную прибыль, если b i = v i .

Доказательство.Если участник i получает товар, следовательно, его ставка b i была самой высокой. Поскольку мы имеем дело с аукционом второй цены, то стоимость товара равна самой высокой из оставшихся ставок:

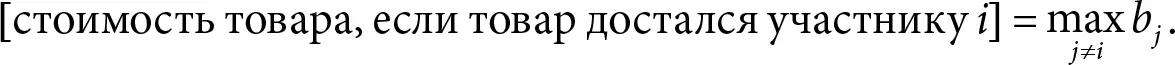
При этом ценность товара для участника i равна v i . Значит, если участник i получает товар, то его прибыль составит