Андрей Райгородский - Кому нужна математика? Понятная книга о том, как устроен цифровой мир

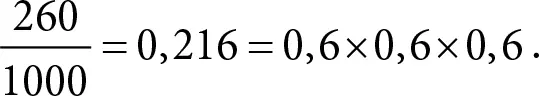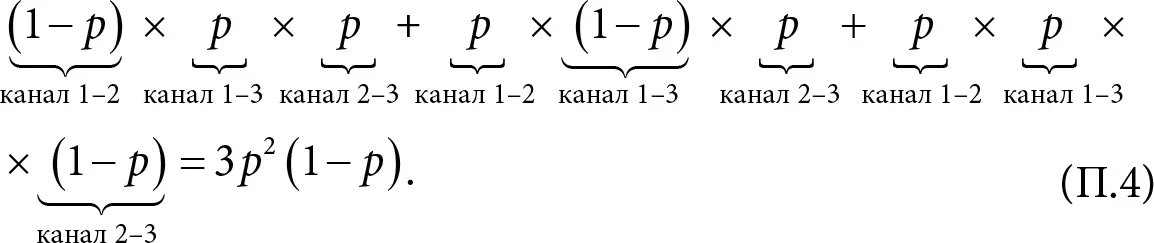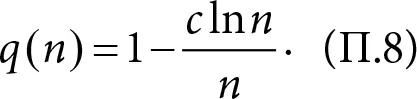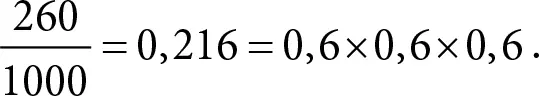
Случай 2. Два канала связи доступны и один недоступен. Недоступным может быть любой из трех каналов связи, поэтому случай 2 можно получить тремя разными способами. В результате соответствующая вероятность равна

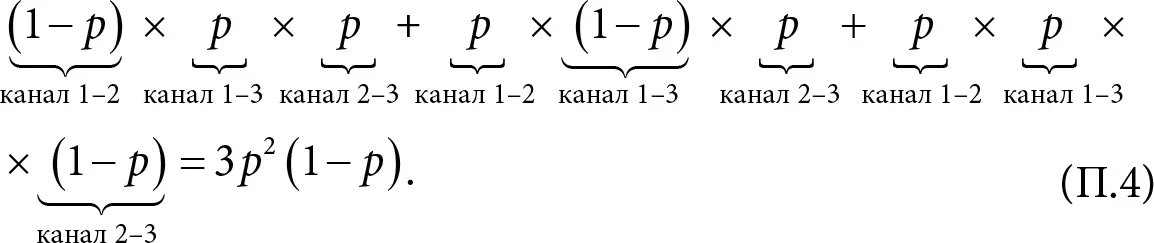
Общая вероятность сохранения связи в сети теперь равна

(П.3) + (П.4) = p ³ + 3 p ² (1 − p ) = 3 p ² −2 p ³.

Потеря связи хотя бы с одним из компьютеров тоже происходит в двух случаях, которые мы назовем случай 3 и случай 4.

Случай 3. Два канала связи недоступны и один доступен. Заметьте, что этот случай совершенно аналогичен случаю 2, только р и ( 1 − p ) поменялись местами. Соответствующая вероятность равна

3 ( p − 1)² p . (П.5)

Случай 4. Все три канала связи недоступны. Этот случай опять же аналогичен случаю 1, если поменять местами р и (1 − p ). Соответствующая вероятность равна

(1 − p )³.(П.6)

Вероятность, что хотя бы один компьютер окажется отрезанным от сети, равна

(П.5) + (П.6) = 3(1 − p )² − 2(1 − p )³.(П.7)

Естественно, если просуммировать все вероятности, то получится единица. Это очень красиво следует из бинома Ньютона третьей степени:

(П.3) + (П.4) + (П.5) + (П.6) = p ³ + 3 p ² (1 − p ) + 3( p − 1)² p + (1 − p )³ = ( p + (1 − p ))³ = 1³ = 1

Если провести еще немножко алгебраических манипуляций, то можно переписать вероятность (П.7) по-другому:

3(1 − p )² − 2(1 − p )³ = (1 − p )² (3 − 2(1 − p )) = (1 − p )² (1 + 2 p ) = (1 − p ) ((1 − p ) (1 + 2 p )) = (1 − p ) (1 + p − 2 p ²)

Легко проверить, что если p > ½, то вторая скобка меньше единицы. Получается, что если p > ½, то вероятность потери связи в мини-сети меньше, чем вероятность потери связи в отдельно взятом канале, которая равна (1 − p ).

Кроме того, выражение (П.7) всегда меньше, чем 3 (1 − p )². Поэтому если вероятность неисправности канала (1 − p ) уменьшается, то вероятность потери связи в сети уменьшается еще быстрее. Когда вероятность (1 − p ) очень мала, то термином −2 (1 − p )³ можно пренебречь. Тогда вероятность потери связи в сети приблизительно равна 3 (1 − p )². Если (1 − p ) = 0,01 (то есть 1 %), то эта формула верна до третьего знака после запятой, что мы и видим в последней строчке табл. 4.1.

Теорема (Эрдеша – Реньи). Допустим, граф состоит из п вершин. Предположим, что ребра независимы друг от друга и любые две вершины соединены ребром с вероятностью р(п). Обозначим вероятность помехи через q(n) = 1 − p(n) и предположим, что

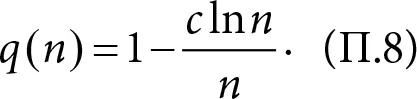
(i) Если c > 1 , то вероятность связности стремится к единице при п, стремящемся к бесконечности, причем скорость стремления к единице тем выше, чем больше число с. Например, при c ≥ 3 скорость стремления к единице не ниже, чем у выражения 1 − 1/ n, как в разделе «Результат Эрдеша – Реньи» в главе 4.

(ii) Если c < 1 , то вероятность связности стремится к нулю при п, стремящемся к бесконечности, причем скорость стремления к нулю тем выше, чем меньше число с.

(iii) При c = 1 вероятность связности стремится не к нулю и не к единице, а к числу e −1≈ 0,3679, где e = 2,71828… – основание натурального логарифма.

Допустим, граф состоит из n вершин. Предположим, что ребра независимы друг от друга и любые две вершины соединены ребром с вероятностью р(п). Обозначим вероятность помехи через q ( n ) = 1 − p ( n ). Рассмотрим одну вершину. Вероятность того, что она не соединена ребром ни с одной из оставшихся n − 1 вершин, равна