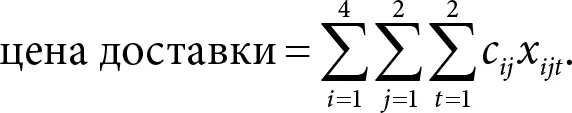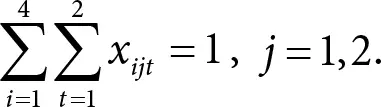Андрей Райгородский - Кому нужна математика? Понятная книга о том, как устроен цифровой мир

Очевидно, что это доказательство легко обобщить на любое количество n переменных.

Допустим, нам нужно отправить грузовики с товаром к двум разным клиентам. Всего у нас в разных точках четыре грузовика. Обозначим через cij цену отправки грузовика i =1,2,3,4 к клиенту j =1,2. На любую доставку требуется полдня. Доставку можно осуществить либо утром (первая половина дня), либо днем (вторая половина дня). Нужно решить, к какому клиенту какой грузовик поедет и в какой момент времени.

Введем переменные x ijt, i =1,2,3,4; j =1,2; t =1,2. Эти переменные могут принимать значение 0 или 1. Например, если грузовик 3 едет к клиенту 2 в первой половине дня, то x 321=1. Если этого не происходит (то есть грузовик 3 в первой половине дня никуда не едет или едет к другому клиенту), то x 321=0.

В нашей небольшой задаче всего 4×2×2=16 переменных, то есть ее можно решить и вручную.

Целевая функция – это цена доставки, и вычисляется она очень просто:

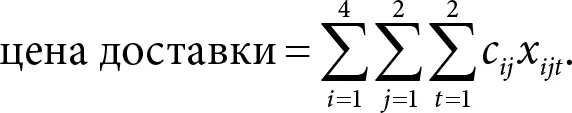
Например, если грузовик 3 едет к клиенту 2 в первой половине дня, то x 321= 1 и мы прибавим к общей стоимости c 32. А если грузовик 3 к клиенту 2 не поедет, тогда x 321= x 322= 0 и c 32не войдет в общую сумму.

Самое интересное – это ограничения. Например, грузовик i не может поехать к двум клиентам в одно и то же время. Это можно записать в виде ограничения:

x i1t+ x i2t≤, i =1,2,3,4; t =1,2.

Тогда для любого i и t только одно (или ни одно) из значений х i1tили х i2tможет равняться единице.

Еще одно универсальное ограничение: к клиенту j нужно послать только один грузовик, то есть

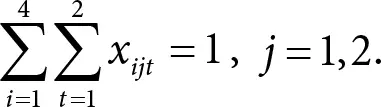
Ограничения могут учитывать особенности каждого грузовика, клиента и другие факторы. Например, мы не хотим, чтобы грузовик 3 работал утром (скажем, у этого грузовика запланирован техосмотр). Тогда мы просто включим ограничение:

x 311+ x 321= 0.

Теперь допустим, что это условие желательное, но необязательное. Тогда к целевой функции можно добавить дополнительное слагаемое, которое будет означать штраф за невыполнение условия:

c штраф( x 311+ x 321).

Заметьте, что это слагаемое действительно добавится, только если грузовик 3 работал в утреннюю смену. Естественно, оптимальное решение будет зависеть от коэффициента c штраф. Если он больше любого c ij в целевой функции, то оптимальный вариант – не задействовать грузовик 3 с утра. А если коэффициент с штрафмаленький, то, возможно, грузовик 3 все равно задействуют, если это обеспечит более низкую цену доставки.

В виде линейных ограничений можно записать самые разные условия. Например, мы хотим, чтобы грузовик 3 либо работал, либо не работал обе половины дня. Тогда мы вводим ограничение

x 311+ x 321= x 312+ x 322.(П.2)

Это условие можно несколько усложнить. Например, если грузовик 3 в первой половине дня поехал к клиенту 1, то мы хотим, чтобы он работал и во второй половине дня. Как это записать в виде линейного неравенства? Часто используется такой прием. Вводим достаточно большое значение М и записываем:

( x 311+ x 321) − ( x 312+ x 322) ≤ M (1 − x 311).

Если x 311=1, то значение справа при любом М равно нулю. Тогда неравенство выполняется (и на самом деле является равенством), только если x 312+ x 322=1 (вспомните, что x 311+ x 321=1). Но если x 311=0, то М можно выбрать достаточно большим, чтобы ограничение не играло никакой роли. В данном случае, кстати, достаточно, чтобы М =1. Для увеличения скорости решения М стараются выбирать «экономно» – не больше, чем нужно.

Есть еще множество интересных приемов записи обязательных и желательных условий в виде линейных выражений, но их более подробное описание выходит за рамки нашей книги.