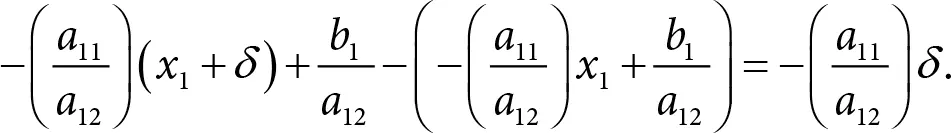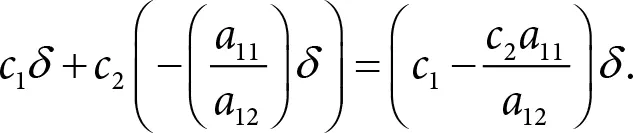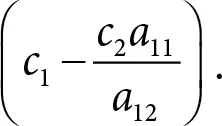Андрей Райгородский - Кому нужна математика? Понятная книга о том, как устроен цифровой мир

Отметим, что в выражении стоимости 1020 − 2 × АЮ − 5 × БЮ в нашем примере оптимальные значения АЮ и БЮ не зависят от слагаемого 1020. Решение будет то же, если мы будем минимизировать −2 × АЮ − 5 × БЮ или максимизировать 2 × АЮ + 5 × БЮ.

Рассмотрим задачу линейного программирования с двумя переменными в общем виде.

Заметьте, что, во-первых, задача максимизации эквивалентна задаче минимизации с коэффициентами − с 1и − с 2. Во-вторых, любое неравенство со знаком ≤ можно превратить в эквивалентное неравенство со знаком ≥, умножив обе части неравенства на –1. Поэтому задача выше, для двух переменных и m ограничений, сформулирована действительно в общем виде. Все значения коэффициентов a, b, с – произвольные действительные числа, которые могут быть как положительными, так и отрицательными.

Каждое ограничение задает полуплоскость значений, на которой оно выполняется. Если пересечение всех m полуплоскостей пусто, то допустимого решения просто не существует. Поэтому допустим, что m полуплоскостей содержат общую ограниченную область S допустимых значений. (Мы не будем рассматривать случай, когда область не ограничена.) Очевидно, что S – это многоугольник, поскольку область S ограничена прямыми.

Утверждение. Максимальное значение целевой функции достигается в одном из углов S.

Доказательство.Обозначим оптимальное решение через x * 1, x * 2. Заметьте, что x * 1, x * 2не может быть внутренней точкой S, потому что в этом случае оба значения переменных можно либо увеличить, либо уменьшить, таким образом увеличивая значение целевой функции. Например, в нашей задаче в главе 2решение (58,8) является внутренней точкой, поэтому не может быть оптимальным.

Значит, x * 1, x * 2лежит на одной из сторон многоугольника S. На каждой из сторон одно из ограничений превращается в равенство. Рассмотрим сторону, которая соответствует первому ограничению: a 11 x 1+ a 12 x 2= b 1. Что происходит, если мы начнем двигаться вдоль этой стороны?

Не уменьшая общности, допустим, a 12≠ 0. Для начала перепишем равенство в более привычном виде как уравнение прямой:

Допустим, мы начали в точке ( x 1, x 2). Теперь допустим, что мы немного изменили х 1и получили новую координату x 1+ δ , где δ >0 достаточно мало, чтобы все остальные ограничения, кроме первого, по-прежнему строго выполнялись. Тогда значение х 2изменится на величину

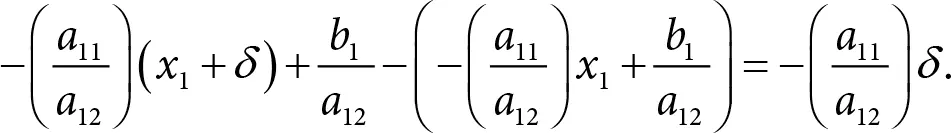
При этом нетрудно проверить, что целевая функция изменится на величину

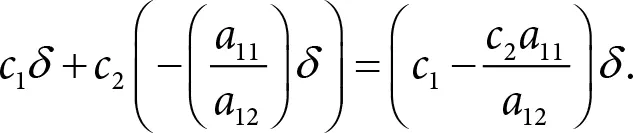
Заметьте, что это число не зависит от ( x 1, x 2). Значит, в какой бы точке прямой (П.1) мы не начали движение, в результате перемещения по этой прямой, изменение значения целевой функции зависит только от коэффициента

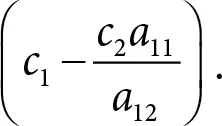
Если он отрицательный, то, увеличивая x 1и двигаясь по прямой, мы можем только уменьшить целевую функцию. Аналогично если коэффициент положительный, то, двигаясь по прямой в сторону увеличения x 1, мы можем целевую функцию только увеличить. Наконец, если коэффициент равен нулю, значение целевой функции на всей прямой постоянно.

Стало быть, из любой точки на данной стороне S мы можем двигаться либо в сторону уменьшения, либо в сторону увеличения x 1так, чтобы значение целевой функции не уменьшалось. Таким образом мы можем менять значение x 1, пока какое-то другое ограничение не превратится в равенство. В этом случае мы столкнулись с углом многоугольника S, в котором достигается максимальное значение целевой функции на всей рассмотренной нами стороне. Поскольку сторону мы выбрали произвольно, делаем вывод, что максимальное значение целевой функции достигается в одном из углов S и мы можем выбрать этот угол в качестве x * 1, x * 2.