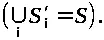Виталий Сигорский - Математический аппарат инженера

Входная последовательность называется допустимой для автомата в состоянии s i , если она не нарушает ограничений на входе ни в каком состоянии автомата М и порождаемый ею выход определен на заключительном такте. На других тактах входной последовательности выходы могут быть и не определены, но последовательность состояний обязательно должна существовать. Например, для приведенного автомата в состоянии 0 допустимая входная последовательность {0, 1,0} порождает последовательность состояний {1, 4, 5} и заключительный выход 0. В то жевремя последовательность {0, 1, 1} не допустима, так как заключительный выход не определен.

Число состояний неполного автомата иногда можно сократить изложенными в предыдущих разделах методами, произвольно интерпретируя прочерки в его таблице и рассматривая его как полный автомат. Однако такой путь не гарантирует получения минимальной формы.

Сокращенная форма неполного автомата М – это такой автомат М', который по отношению к допустимым для М входным последовательностям ведет себя на выходах так же, как и исходный автомат М, но имеет меньшее число состояний. Автомат М' квазиэквивалентен автомату М. Отношениеквазиэквивалентности рефлексивно и транзитивно, но не симметрично, т. е обладает всеми свойствами отношения включения. Поэтому говорят также, что М' включает М и записывают М ⊂М'. При этом из М ⊂М' вовсе не следует М' ⊂М, что иногда выражают словами: М' делает столько же и, быть может, больше, чем М.

10. Минимизация неполных автоматов. Эта задача сводится к поиску квазиэквивалентного автомата, который имеет наименьшее число состояний, и решается следующим образом.

Сначала на множестве состояний S = { σ 1 , σ 2 , ..., σ r} исходного автомата определяется отношение совместимости. Состояния σ i и σ j называют совместимыми, если любая допустимая для этих состояний входная последовательность не порождает различных заключительных выходов при начальных состояниях σ i и σ j автомата. Отношение совместимости рефлексивно и симметрично, однако оно не обязательно транзитивно. Отсюда следует, что совместимость является отношением толерантности. Все совместимые между собой состояния объединяются в классы толерантности S ' 0, S ' 1, ..., S ' w , которые образуют некоторое покрытие множества состояний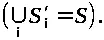

Для определения совместимых состояний можно воспользоваться методом, аналогичным изложенному для полных автоматов. Исходная таблица содержит пары таких состояний, при которых для любого допустимого

- 578 -

символа отсутствуют различные выходы. Клетки, соответствующие запрещенным входам для данной пары состояний, заполняются прочерком и при исключении пар, как это описано в (8), не учитываются. Так, для автомата, заданного табл. 12, имеем:

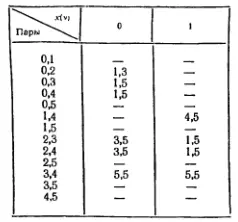
Отмеченная на первом шаге пара {0, 2} является единственной несовместимой парой в таблице, так как она не содержится ни в каких других строках. Следовательно, всенеотмеченные пары являются совместимыми. Построив матрицу толерантности для совместимых пар и переставив в ней строки и столбцы, имеем:

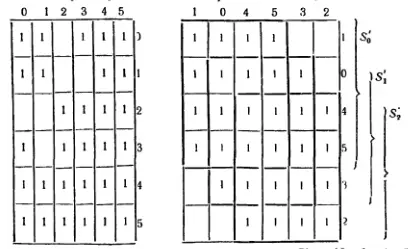
Отсюда выделяем кассы толерантности S ' 0= {0, 1, 4, 5}, S ' 1= {0, 3, 4, 5} S ' 2= {2, 3, 4, 5}, объединяющие совместимые между

- 579 -

собой состояния. Здесь, в частности, можно убедиться в том, что совместимость не обладает свойством транзитивности. Например, пары состояний {0, 1} и {0, 3} совместимы, но состояния 1 и 3 не входят в один и тот же класс толерантности и, следовательно, они несовместимы.

Из определения совместимости и способа получения классов толерантности следует, что при воздействии любого не запрещенного входного символа автомат из совместимых состояний переходит в одно и то же или в совместимые состояния, а выходы (если они определены) при этом будут одинаковы.

Так, в нашем примере при воздействии 0 классы S' 0 и S' 1 переходят в {1, 5}, а S' 2 – в {3, 5}; при воздействии 1 класс S' 0 переходит в {4, 5}, S' 1 – в {5} и S' 2 – в {1, 5}. Следовательно, исходный автомат можно представить квазиэквивалентным ему автоматом, в котором классам совместимости S' 1, S 2,..., S' w соответствуют состояния σ' 0, σ' 1, ..., σ' w. Однако такой автомат не всегда будет минимальным. Для получения минимальной формы автомата необходимо отобрать наименьшее число таких классов совместимости, которые образуют покрытие множества состояний S и в то же время включают множества состояний, следующих за состояниями каждого класса при всех незапрещенных воздействиях. Для рассматриваемого примера этим требованиям удовлетворяют классы S' 0 и S' 1 , так как S' 0∪ S' 2= S , и все множества последующих состояний {1, 5}, {3, 5}, {4, 5} и {5} являются подмножествами S' 0 и S' 2 . Соответствующая минимальная форма показана на рис. 241, б, где состояния 0 и 1 соответствуют классам S' 0 и S' 2 .