Виталий Сигорский - Математический аппарат инженера

- 568 -

поэтому дуга из вершины 0 в 1 помечается как 2 / 0. Переход в состояние 2 совершается под воздействием 1 и ему соответствует выход 0, поэтому дуга из вершины 0 в 2 помечается как 1/0. Переходы в состояние 3 совершаются под воздействиями 0 и 3 и им обоим соответствует выход 0, поэтому дуга из вершины 0 в 3 помечается как дизъюнкция 0/0 Ú 3/0. Аналогично определяются и другие дуги графа. Петли соответствуют переходам, при которых состояния не изменяются. Так, рассматриваемый автомат переходит из состояния 2 в 2 под воздействиями 1 и 2, которым соответствуют выводы 0 и 1. Следовательно, петля при вершине 2 помечается как дизъюнкция 1/0 Ú 2/1.

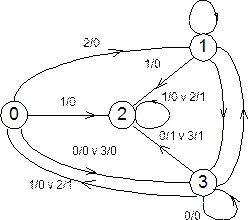
Рис. 236. Граф конечного автомата.

Матрица соединения автомата М (или матрица переходов ) представляет собой квадратную таблицу в которой номера строк и столбцов соответствуют номерам состояний. Клетка матрицы на пересечении i -й строки и j -го столбца заполняется дизъюнкцией пар «вход — выход», которая приписана дуге графа исходящей из i- й в j -ю вершину. При отсутствии такой ветви клетка заполняется нулем или остается свободной. Так для рассматриваемого примера имеем:

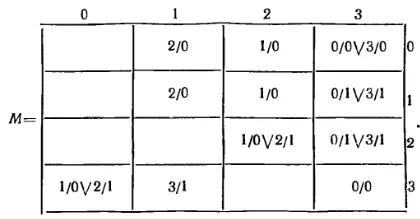
5. Анализ конечных автоматов. Полное описание поведения автомата заключается в определении последовательности выходных сигналов при возбуждении его в тактовые моменты времени некоторой последовательностью входных сигналов. Входная и выходная последовательности представляются наборами символов (или их номеров) из алфавитов Х и Y одинаковой длины l . Для такого описания, кроме характеристических функций, необходимо определить или задать начальное состояние автомата.

Наиболее удобно определять реакцию автомата на входною последовательность по его графу. Для этого достаточно проследить

- 569 -

путь в графе, начиная от вершины начального состояния, по направлению дуг, которые отмечены очередными номерами на входной последовательности. Выходная последовательность определяется номерами, которыми отмечены дуги в порядке их следования по пройденному пути, а последовательность состоянии автомата номерами вершин, через которые проходит этот путь.

Так, из графа на рис. 236 для входной последовательности (2, 0, 1, 1, 2, 3) и начального состояния 0 имеем выходную последовательность (0, 1, 0, 0, 1, 1) и смену состояний автомата (1, 3, 0, 2, 2, 3). При начальном состоянии 2 и той же входной последовательности получаем соответственно (1, 1, 0, 0, 1, 1) и (2, 3, 0, 2. 2, 3).

С помощью графа автомата легко выделить следующие характерные типы его состояний:

1) преходящее состояние, из которого можно перейти, но крайней мере, в одно другое состояние, но после этого уже нельзя возвратиться в него ни при каком воздействии (соответствующая вершина не имеет заходящих дуг, но имеет хотя бы одну исходящею дугу);

2) тупиковое состояние, в которое можно перейти, по крайней мере, из одного другого состояния, но после этого уже нельзя выйти из него ни при каком воздействии (соответствующая вершина не имеет исходящих дуг в другие вершины, но имеет хотя бы одну входящую дугу из другой вершины);

3) изолированное состояние, из которого нельзя перейти ни в какое другое состояние и в него нельзя попасть ни из какого другого состояния (соответствующая вершина содержит только петлю).

Аналогичные определения можно дать для некоторых совокупностей состояний, рассматриваемых как подавтоматы. Если начальное состояние автомата М принадлежит непустому множеству S i состояний, которое составляет тупиковый или изолированный подавтомат, то M можно упростить исключением всех состояний, которые не принадлежат множеству S i , и всех дуг, начинающихся в этих состояниях.

Пусть М 1, М 2 и M 3- соответственно преходящий, тупиковый и изолированные подавтоматы автомата М, которые характеризуются множествами состояний S 1 , S 2 и S 3 . Очевидно, выделение таких подавтоматов соответствует разбиению множества S состояний автомата М на непересекающиеся подмножества S 1 , S 2 и S 3 , представляющие собой классы эквивалентности ( S 1∪ S 2∪ S 3= S и S 1∩ S 2∩ S 3= ∅ ). Как следует из обобщенного графа (рис. 237), матрица соединения автомата может быть представлена в виде: