Виталий Сигорский - Математический аппарат инженера

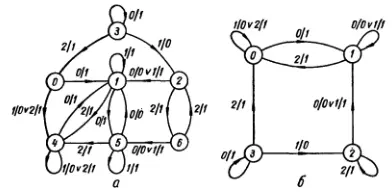
Рис. 240. Граф конечного автомата ( а ) и его сокращенная форма ( б )

Минимизация числа состоянии полных автоматов связана с отношением эквивалентности. Пусть автоматы М 1 и М 2 , находящиеся соответственно в начальных состояниях, σ iи σ j(обозначения М 1 и М 2 могут относиться к одному и тому же автомату), под воздействием любой входной последовательности выдают одинаковые выходные последовательности, т. е. автоматы М 1 и М 2 в данных состояниях σ iи σ jнеразличимы по внешним выходам. Такое отношение между состояниями одного и того же или двух различных автоматов обладает свойствами рефлексивности, симметричности и транзитивности, следовательно, оно является отношением эквивалентности состояний. Если состояния не эквивалентны, то их называют различимыми. Легко доказать справедливость следующих положений:

1) состояния σ iи σ jавтомата явно различимы, если различаются соответствующие, им строки в таблице выходов;

2) состояния σ iи σ jавтомата явно эквививалентны, если соответствующие им строки в таблице переходов и таблице выходов одинаковы или становятся одинаковыми при замене каждого номера σ iна номер σ j(или наоборот).

Например, для автомата, граф которого изображен на рис. 240, а , общая таблица переходов имеет вид:

- 573 -

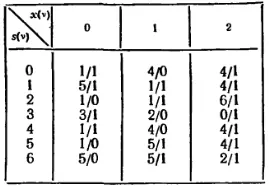
Из этой таблицы следует, что состояния из множества {0, 3, 4}являются явно различимыми с любым состоянием из множества {1, 2, 5, 6}. Поэтому следует искать эквивалентные состояния только среди элементов, принадлежащих одному из этих множеств. Так как строки 0 и 4 одинаковы, а строки 1 и 5 становятся одинаковыми при замене цифры в числителе 1 на 5 (или 5 на 1), то явно эквивалентными являются пары состояний {0,4} И {1,5}.

Объединяя эквивалентные состояния в автомате М 1 , получаем эквивалентный автомат М 2 с меньшим числом состоянии, который в любом состоянии нельзя отличить от исходного, наблюдая сигналы на выходах. Очевидно, автоматы М 1 и М 2 являются эквивалентными, если каждому состоянию σ i, автомата М 1 соответствует, по крайней мере, одно эквивалентное ему состояние автомата M 2 , и если каждому состоянию σ j, автомата М 2 соответствует хотя бы одно эквивалентное ему состояние автомата М 1.

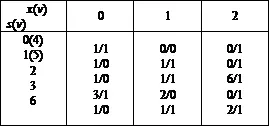
Эквивалентные состояния, например, σ iи σ j, удобно объединять по общей таблице переходов, вычеркивая строку σ j, и заменяя везде в числителе числа σ jна σ i. После объединения пар явно эквивалентных состояний может оказаться возможным снова обнаружить такие состояния, которые также объединяются с помощью аналогичной процедуры. В результате последовательного объединения приходим к сокращенной таблице переходов, которой соответствует сокращенный автомат, эквивалентный исходному, но имеющий меньшее число состоянии. Так, для рассматриваемого примера получаем последовательно:

- 574 -

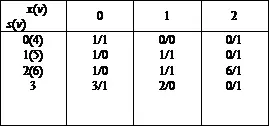
Первая таблица соответствует объединению пар эквивалентных состоянии {0,4} и {1, 5}, а вторая - объединению пары {2, 6}. Сокращенный автомат содержит только четыре состояния (рис.240, б).

8. Эквивалентное разбиение. Если известны все пары эквивалентных состояний конечного автомата, то тем самым на множестве S его состояний определено отношение эквивалентности, которому соответствует некоторое разбиение на классы эквивалентности S = {S 1, S 2..., S ν } . При этом состояние, не имеющее эквивалентного ему состояния, составляет класс эквивалентности, единственным элементом которого является это состояние. Обозначим через σ ' 0, σ ' 1, ..., σ ' νпредставители классов эквивалентности и через М' – автомат, множеством состояний которого является семейство представителей S '= {σ ' 0, σ ' 1, ..., σ ' ν}. Можно утверждать, что автоматы М и М' эквивалентны ( М ~ М' ), причем М' имеет минимальное число состояний, т. е. является минцмальной формой автомата.

Объединение эквивалентных состояний в классы эквивалентности осуществляется весьма просто. Если σ i ~ σ j и σ j ~ σ k, то на основе свойства транзитивности следует, что σ i ~ σ k , и, значит, пары { σ i , σ j} и { σ j , σ k} входят в общий для них класс эквивалентности. Но для выявления всех пар эквивалентных состояний требуется более громоздкая процедура, так как множество таких пар не исчерпывается явно эквивалентными состояниями и не всегда может быть полностью обнаружено и объединено способом, изложенным ранее.