Виталий Сигорский: Математический аппарат инженера

2. Состояния.Кроме входных и выходных переменных, можно выделить некоторую совокупность промежуточных переменных, которые связаны с внутренней структурой автомата. В комбинационных схемах промежуточные переменные непосредственно не участвуют в соотношениях вход - выход. Напротив, выходные функции последовательностных схем в качестве своих аргументов, кроме входных переменных, обязательно содержат некоторую совокупность промежуточных переменных s 1, s 2, …, s k, характеризующих состояние схемы. Набор всех возможных состоянии, которые присущи данной схеме, называется множеством состояний. Если S 1, S 2, …, S k- конечные алфавиты переменных состояния s 1, s 2, …, s k, то множество состояний S = S 1× S 2× … × S kтакже является конечным множеством.

Строгое определение понятия состояния связывается с той ролью, которое оно играет при описании конечных автоматов. Во-первых, значения совокупности выходных переменных на ν -м такте у ( ν ) = ( y 1 ( ν ), y 2 ( ν ), …, y m ( ν )), однозначно определяется значениями входных переменных x( ν ) = ( x 1 ( ν ), x 2 ( ν ), …, x n ( ν )) и состоянием s( ν ) = ( s 1 ( ν ), s 2( ν ), …, s k ( ν )), на том же такте, т.е. у ( ν ) = λ (x( ν ), s( ν )). Во-вторых, состояние s( ν + 1) в следующем ( ν + 1)-м такте однозначно определяется входными переменными х ( ν ) и состоянием s( ν ) в предыдущем такте, т.е. s( ν + 1) = δ (x( ν ), s( ν )).

Таким образом, состояние конечного автомата в любой тактовый момент характеризуется значениями такой совокупности переменных, которая вместе с заданными значениями входных переменных позволяет определить выходные переменные в данный тактовый момент и состояние в следующий тактовый момент.

- 565 -

Ясно, что последовательностные схемы должны обладать способностью сохранять предыдущее состояние до следующего такта, в связи с чем их называют также автоматами с памятью или последовательностными машинами. В качестве памяти могут использоваться элементы задержки, на выходах которых повторяются входные воздействия со сдвигом во времени на интервал между тактами D t . Широко применяются также различные запоминающие элементы, например, триггеры, способные сохранять состояния на выходах до тех пор, пока оно не изменяется в результате воздействия на их входы.

3. Типы конечных автоматов.В технике с понятием автомата обычно связывается некоторое устройство, способное выполнять определенные функции без вмешательства человека или с его ограниченным участием. Однако такое понимание является слишком узким. В широком смысле конечный автомат - это математическая модель, отображающая физические или абстрактные явления самой разнообразной природы. Такая модель успешно используется как в технике (проектирование электронных вычислительных машин, систем управления и связи), так и в других областях - психологии и физиологии (исследование деятельности нервной системы человека и простейших видов поведения животных), лингвистике (анализ синтаксиса русского, английского или других языков, расшифровка древних рукописей), теории и практике административного управления и т.п. Универсальность теории автоматов позволяет рассматривать с единой точки зрения различные объекты, устанавливать связи и аналогии между ними, переносить результаты из одной области в другую.

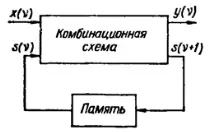
Рис. 235. Блок-схема конечного автомата.

Конечный автомат М определяется как система с конечным входным алфавитом Х = { ξ 1, ξ 2, ... , ξ p}, конечным выходным алфавитом Y = { v 1, v 2, …, v q}, конечным множеством состояний S = {σ 1, σ 2, ..., σ i}, и двумя характеристическими функциями:

s(ν + 1) = δ (x(ν), s(ν));

у (ν) = λ ( х (ν) , s (ν)),

называемыми соответственно функцией переходов и функцией выходов. Общая блок-схема конечного автомата (рис. 235) может быть представлена в виде комбинационной схемы, реализующей характеристические функции δ и λ, и памяти, сохраняющей на один такт предыдущее состояние автомата.

В определении автомата участвует три конечных множества X, Y, S и две функции δ и λ, задающие некоторые отношения между

- 566 -

элементами этих множеств. Следовательно, конечный автомат можно обозначить упорядоченной пятеркой М = (X, Y, S, δ, λ). Мощности множеств X , Y, S равны соответственно: