Виталий Сигорский: Математический аппарат инженера

,

- 570 -

где μ 11, μ 22, μ 33- матрицы подавтоматов М 1, М 2 и М 3; μ 12- матрица, характеризующая переходы от состояний преходящего автомата М 1 к состояниям тупикового автомата М 2. Отсюда следует, что разбиение автомата М на подавтоматы М 1, М 2 и М 3 можно осуществить преобразованием его матрицы соединений к стандартному виду путем перестановки соответствующих строк и столбцов. Например, для автомата, граф которого изображен на рис. 238, имеем:

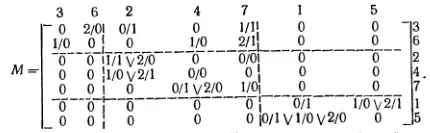
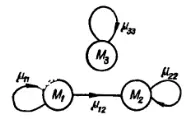
Рис. 237. Обобщенный граф конечного автомата.

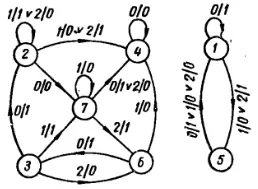
Рис. 238. Граф конечного автомата к примеру разбиения на подавтоматы.

Отсюда следует, что S 1 = {3, 6} составляет преходящий подавтомат, S 2 = {2, 4, 7} - тупиковый подавтомат и S 3 = {1, 5} - изолированный подавтомат. Если начальное состояние принадлежит множеству S 2 , то можно упростить автомат, исключив состояния S 1∪ S 3= {3, 6, 1, 5}, а в случае принадлежности начального состояния множеству S 3 автомат упрощается исключением состояний S 1∪ S 2= {3, 6, 2, 4, 7}.

6. Синтез конечных автоматов.Реализация конечных автоматов сводится к синтезу соответствующей комбинационной схемы, преобразующей входные переменные x( ν ) и s( ν ) в выходные переменные y ( ν ) и s( ν + 1) в соответствии с заданными характеристическими функциями s( ν + 1) = δ (x( ν ), s( ν )) и y ( ν )= λ (x( ν ), s( ν )). Для сохранения состояний s( ν + 1) до следующего такта в цепь обратной связи вводится необходимое количество элементов памяти.

При реализации автоматов в двоичном структурном алфавите можно использовать рассмотренные ранее методы синтеза

- 571 -

комбинационных схем. Но для этого необходимо закодировать состояния схемы н представить характеристические функции в виде булевых функций двоичных переменных. Такое кодирование можно осуществить преобразованием общей таблицы перехода автомата к таблице соответствия в двоичном структурном алфавите. Если элементы множеств X , Y и S пронумерованы порядковыми числами, начиная с нуля, то им соответствуют коды, представляющие собой двоичные эквиваленты этих чисел. Например, для автомата, заданного в (4), таблицу переходов можно преобразовать к виду:

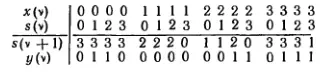
Заменяя десятичные числа их двоичными эквивалентами, читаемыми сверху вниз, получаем таблицу соответствия, в которой значения функций s( ν + 1) и у ( ν ) представлены двоичными кодами:

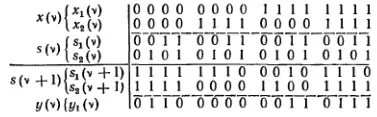
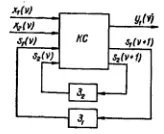
Рис. 239. Структурная схема конечного автомата

Отсюда видно, что комбинационная схема должна иметь четыре входа, соответствующие входным переменным x 1 ( ν ), х 2 ( ν ) и переменным состояния s( ν ), s 2( ν ) , а также три выхода, соответствующие переменным состояния s 1 ( ν + 1), s 2( ν + 1) и выходной переменной у 1 ( ν ). Синтезировав комбинационную схему, соответствующую полученной таблице и введя два элемента задержки З 1и З 2, получим структурную схему автомата (рис. 239).

7. Минимизация автоматов.С утилитарной точки зрения интерес представляет только зависимость между входами и выходами автомата, а роль его состоянии сводится исключительно к участию в формировании этих зависимостей в качестве промежуточных переменных. Следовательно, любая совокупность состояний, обеспечивающая требуемые зависимости между входом и выходом, может быть выбрана в качестве множества состоянии автомата. В то же

- 572 -

время этот выбор естественно подчинить определенным целям, например, минимизации числа состояний или оптимизации автомата в каком-либо смысле. Следует иметь в виду, что с уменьшением числа состоянии уменьшается и количество требуемых элементов памяти, но это может привести к усложнению комбинационной схемы автомата. Поэтому синтез наиболее экономичного автомата часто требует поиска удачного компромисса между сложностью его комбинационной и запоминающих частей.