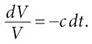
Здесь коэффициент пропорциональности c – это скорость выведения, мера того, насколько быстро организм избавляется от вируса.
Приведенное уравнение – пример дифференциального уравнения. Оно связывает дифференциал функции dV с самой функцией V , а также с дифференциалом dt времени. Проинтегрировав обе части с помощью основной теоремы, Перельсон и Хо решили его относительно V ( t ) и обнаружили, что справедливо соотношение
ln[ V ( t ) / V 0] = – ct ,
где V 0 – первоначальная вирусная нагрузка, а ln – натуральный логарифм (та самая логарифмическая функция, которую изучали Ньютон и Меркатор в 1660-е годы). Отсюда можно найти, что
V ( t ) = V 0 e - ct ,
где e – основание натуральных логарифмов. Это подтверждало, что вирусная нагрузка в модели действительно снижалась экспоненциально. Наконец, подобрав экспоненту в соответствии с экспериментальными данными, Хо и Перельсон оценили ранее неизвестное значение скорости выведения c .
Для тех, кто предпочитает использовать производные, уравнение модели можно записать так:
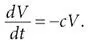
Здесь dV / dt – это производная V . Она показывает, насколько быстро растет или падает концентрация вируса. Положительное значение производной означает повышение, отрицательное – снижение. Поскольку концентрация V положительна, величина – cV должна быть отрицательной, поэтому и производная должна быть отрицательной, что означает снижение концентрации, как и показал эксперимент. Кроме того, пропорциональность между dV / dt и V означает, что чем ближе V к нулю, тем медленнее спад. На интуитивном уровне это замедление спада V подобно тому, что происходит, когда вы наполняете раковину водой, а затем открываете сток. Чем меньше воды в раковине, тем медленнее она стекает, поскольку уменьшается давление воды, заставляющее ее течь. При такой аналогии количество вируса подобно количеству воды, а стекание – оттоку вируса в результате работы иммунной системы.
Смоделировав действие ингибитора протеазы, Перельсон и Хо скорректировали свое уравнение, чтобы описать условия до введения препарата. Они предположили, что уравнение будет иметь вид
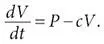
В этом уравнении P означает исходный (не замедленный) темп репродукции вирусных частиц – еще один параметр, неизвестный в то время. Перельсон и Хо предполагали, что до введения ингибитора протеазы в каждый момент зараженные клетки продуцировали новые вирусные частицы, которые потом заражали новые клетки, и так далее. Именно возможность такого взрывного распространения и делает ВИЧ настолько разрушительным.
Однако на бессимптомной стадии, похоже, существует некое равновесие между воспроизводством вируса и его выведением иммунной системой. На этом установившемся уровне вирус размножается с такой же скоростью, как и выводится. Это позволило понять, почему вирусная нагрузка может не меняться годами. В аналогии с водой это подобно происходящему при одновременном открытии и крана, и стока. Вода достигает стабильного уровня, когда поступление жидкости равно ее оттоку.
Если на некотором уровне концентрация вируса не меняется, то ее производная должна быть равна нулю: dV / dt = 0. Следовательно, стабильная вирусная нагрузка удовлетворяет соотношению
P = cV 0.
Перельсон и Хо использовали это простое уравнение, чтобы оценить жизненно важный параметр, который никто не мог измерить ранее: количество вирусных частиц, ежедневно удаляемых иммунной системой. Оказалось, что эта величина – миллиард вирусных частиц в день.
Число получилось неожиданно огромным и впечатляющим. Оно указывало на то, что во внешне, казалось бы, спокойные десять лет бессимптомной стадии в организме больного ежедневно происходит титаническая борьба. Каждый день иммунная система выводит миллиард вирусных частиц, а зараженные клетки порождают миллиард новых. Иммунная система вела яростную тотальную войну с вирусом и боролась с ним практически до полной остановки.
Читать дальше
Конец ознакомительного отрывка
Купить книгу
![Стивен Строгац Бесконечная сила [Как математический анализ раскрывает тайны вселенной] обложка книги](/books/438782/stiven-strogac-beskonechnaya-sila-kak-matematicheski-cover.webp)
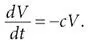
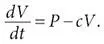







![Стивен Бакстер - Бесконечная утопия [litres]](/books/419234/stiven-bakster-beskonechnaya-utopiya-litres-thumb.webp)


