Это заставило Лейбница задуматься о площадях. Ведь определение площади под какой-то кривой на координатной плоскости сводится к суммированию длинного списка чисел – площадей множества тонких вертикальных прямоугольных полосок.
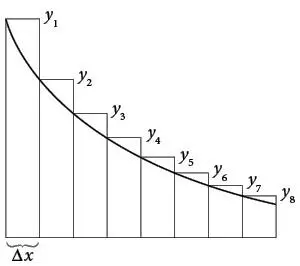
На этом рисунке отражена идея, к которой он пришел. Здесь только восемь прямоугольных полос, но вы должны попробовать представить такую же картинку с миллионами и миллиардами более тонких прямоугольников или, еще лучше, бесконечно много бесконечно тонких прямоугольников. К сожалению, это трудно нарисовать или визуализировать, поэтому-то я и использую только восемь прямоугольников.
Для простоты предположим, что у всех прямоугольников одинаковая ширина. Назовем ее Δ x . Высоты прямоугольников равны y 1, y 2, …, y 8. Тогда общая площадь всех аппроксимирующих прямоугольников составит
y 1Δ x + y 2Δ x + … + y 8Δ x .
Такую сумму восьми чисел было бы удобно «телескопировать», если бы мы нашли какие-нибудь волшебные числа A 0, A 1, A 2, …, A 8, разности которых дают площади прямоугольников
y 1Δ x = A 1 – A 0,
y 2Δ x = A 2 – A 1,
y 3Δ x = A 3 – A 2,
и так далее, вплоть до y 8Δ x = A 8 – A 7. Тогда общая площадь всех прямоугольников телескопически сложилась бы так:
y 1Δ x + y 2Δ x + … + y 8Δ x = ( A 1 – A 0) + ( A 2 – A 1) + … + ( A 8 – A 7) = A 8 – A 0.
А теперь подумайте, что будет, если мы выполним предельный переход к бесконечно узким полоскам. Их ширина Δ x превратится в дифференциал dx . Их переменные высоты y 1, y 2, …, y 8станут y ( x ) – функцией, которая определяет высоту бесконечно узкого прямоугольника, стоящего над точкой x . Сумма бесконечного числа таких прямоугольников станет интегралом ∫ y ( x ) dx . При этом, как и в предыдущих случаях телескопирования, сумма A 8 – A 0превращается в A ( b ) – A ( a ), где a и b – значения x на левом и правом краю области. Вариант телескопирования для бесконечно малых величин дает нам точную площадь под кривой:
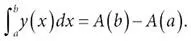
Но как найти эту волшебную функцию A ( x ), которая сделает все это возможным? Что ж, давайте посмотрим на все вышеописанные уравнения вида y 1Δ x = A 1 – A 0. Они превращаются в
y ( x ) dx = dA ,
поскольку прямоугольники становятся бесконечно тонкими. Если записать тот же результат в терминах производных, а не дифференциалов, поделив обе части на dx , то мы получим
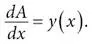
Вот так мы находим аналоги волшебных чисел A 0, A 1, A 2, …, A 8, вызывающих телескопирование. В пределе для бесконечно тонких полосок они определяются неизвестной функцией A ( x ), производная которой – как раз наша функция y ( x ).
Все это – обратная задача и основная теорема анализа в версии Лейбница. Он писал: «Поиск площадей фигур сводится к следующему: по заданному ряду найти суммы или (для лучшего объяснения) по заданному ряду найти другой, разности которого совпадают с членами данного ряда» [248]. Таким образом, разности и телескопические суммы привели Лейбница к дифференциалам и интегралам, а от них – к основной теореме, равно как флюксии и расширяющиеся площади привели Ньютона к тому же тайному источнику.
Борьба с ВИЧ с помощью анализа
Хотя дифференциалы – это измышления разума, с момента их изобретения они весьма глубоко повлияли на наш мир, общество и нашу жизнь. В качестве современного примера рассмотрим вспомогательную роль, которую они сыграли в понимании и лечении ВИЧ, вируса иммунодефицита человека [249].
В 1980-х годах десятки тысяч жизней в США и сотни тысяч по всему миру стала уносить загадочная болезнь. Никто не знал, что это, откуда она взялась и что ее вызывает, но ее воздействие было явным – она настолько ослабляла иммунную систему больных, что они оказывались уязвимы для редких видов рака, пневмонии и оппортунистических инфекций [250]. Смерть от болезни была медленной, мучительной и уродливой. Врачи назвали болезнь синдромом приобретенного иммунодефицита, или СПИДом. Больные и врачи были в отчаянии. Никакого лекарства не просматривалось.
Читать дальше
Конец ознакомительного отрывка
Купить книгу
![Стивен Строгац Бесконечная сила [Как математический анализ раскрывает тайны вселенной] обложка книги](/books/438782/stiven-strogac-beskonechnaya-sila-kak-matematicheski-cover.webp)

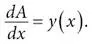







![Стивен Бакстер - Бесконечная утопия [litres]](/books/419234/stiven-bakster-beskonechnaya-utopiya-litres-thumb.webp)


