Сейчас вы, вероятно, думаете: какое отношение имеет альтиметр к исходной задаче сложения большого числа сложных дробей? Ну, прежде всего, если бы мы смогли найти аналог высотомера для сложной суммы, она стала бы легкой. Это было бы эквивалентно разности между показаниями в верхней и нижней точке, что фактически и придумал Лейбниц. Он нашел высотомер для суммы S . Это позволило ему записать каждый член в этой сумме в виде разности двух последовательных показаний высотомера, что, в свою очередь, дало возможность вычислить сумму с помощью вышеописанной идеи. Затем он применил высотомер и к другим задачам. В итоге все это привело Лейбница к основной теореме анализа.
Вооружившись такой аналогией, давайте снова вернемся к сумме S .
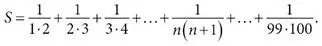
Теперь перепишем каждое слагаемое в виде разности двух других чисел – точно так же, как высота каждой ступеньки была разностью между показанием альтиметра вверху ступеньки и внизу. Начнем с первого слагаемого:
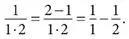
Правда, пока не очевидно, куда это приведет, но оставайтесь с нами. Сейчас мы увидим, насколько полезно переписать дробь 1/(1∙2) в виде разности двух аликвотных дробей 1/1 и 1/2. ( Аликвотной называется дробь, числитель которой равен 1. Эти последовательные дроби станут играть роль последовательных показаний альтиметра.) Если арифметическое преобразование выше кажется неясным, попробуйте воспроизвести его справа налево. Справа мы вычитаем дробь 1/2 из дроби 1/1; в середине приводим их к общему знаменателю; слева упрощаем числитель.
Аналогично мы можем переписать в виде разности двух аликвотных дробей все остальные слагаемые в сумме S :
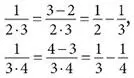
и так далее. В результате наша сумма S примет такой вид:
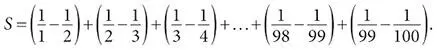
Теперь мы видим метод в этом безумии [247]. Взгляните повнимательнее на структуру суммы. Почти все слагаемые входят в нее дважды, один раз с плюсом, а другой – с минусом. Например, число 1/2 сначала вычитается, а потом добавляется и в результате пропадает. То же верно для 1/3: оно встречается дважды и исчезает. Остальные дроби, до 1/99 включительно, ведут себя так же. Исключения – первое и последнее слагаемое в сумме S , у которых нет парных элементов с другим знаком. В результате, когда дым рассеивается, остаются только они. Поэтому результат таков:
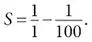
Это вполне логично в свете аналогии с лестницей и снова говорит нам, что общая сумма высот всех ступенек определяется как высота вверху минус высота внизу.
К слову, S упрощается до 99/100. Это и есть ответ на задачу с 99 слагаемыми. Лейбниц понял, что с помощью того же трюка может справиться с любым числом слагаемых. Если в сумме будет N членов, а не 99, то в результате получится:
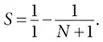
Все это проясняет ответ на изначальный вопрос Гюйгенса: когда N стремится к бесконечности, слагаемое 1/( N + 1) стремится к нулю, а потому S стремится к 1. Следовательно, это предельное значение 1 и будет ответом для задачи Гюйгенса.
Ключевой идеей, позволившей Лейбницу найти эту сумму, была ее весьма конкретная структура: оказалось, что ее можно переписать в виде суммы последовательных разностей (в данном случае в виде разности аликвотных дробей). Такая структура привела к масштабным сокращениям, как мы видели выше. Подобные суммы сегодня в математике называют телескопическими , поскольку они напоминают те старые складные подзорные трубы, которые вы могли видеть в фильмах про пиратов. Аналогия тут в том, что исходная сумма предстает в разложенной форме, но вследствие разностной структуры ее можно привести к более компактному виду. При этом выживают только слагаемые без партнеров, с которыми их можно сократить, – те, которые находятся на концах телескопа.
Естественно, Лейбниц задался вопросом, применим ли трюк с телескопированием к другим задачам. Такую идею стоило реализовать, учитывая, насколько мощной она могла быть. Если бы он, столкнувшись с длинным списком чисел, которые требуется сложить, мог записать каждое число в виде разности последовательных чисел (которые еще нужно определить), телескопический трюк сработал бы снова.
Читать дальше
Конец ознакомительного отрывка
Купить книгу
![Стивен Строгац Бесконечная сила [Как математический анализ раскрывает тайны вселенной] обложка книги](/books/438782/stiven-strogac-beskonechnaya-sila-kak-matematicheski-cover.webp)
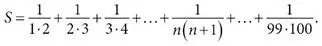
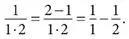
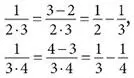
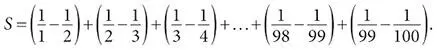
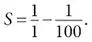
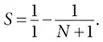







![Стивен Бакстер - Бесконечная утопия [litres]](/books/419234/stiven-bakster-beskonechnaya-utopiya-litres-thumb.webp)


