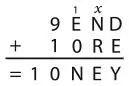Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

Это нам только на пользу, потому что путаница между нолем и буквой «о» только мешает! Однако должен быть перенос в разряде сотен, так как в противном случае E + 0 = N, а значит, E = N, что невозможно, ввиду того что две буквы не могут быть обозначены одним и тем же числом. Теперь сумма выглядит так:

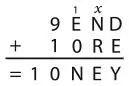
Я прибавил также х там, где должен быть перенос в столбце десятков. Если перенос есть, то х = 1, иначе х = 0. Я прибавил х , потому что это позволяет записать следующие три уравнения, соответствующие оставшимся столбцам.

Столбец сотен: E + 1 = N.

Столбец десятков: + N + R = 10 + E (10 представляет перенос).

Столбец единиц: D + E = Y + 10 х.

Если х = 0, то, подставив E + 1 вместо N во втором уравнении, получим:

E + 1 + R = 10 + E, что можно упростить до R = 9.

Этот результат невозможен, поскольку S = 9. Следовательно, х = 1, что дает нам три уравнения:

E + 1 = N

N + R = 9 + E

D + E = Y + 10

Подставив E + 1 вместо N во втором уравнении, получим E +1 + R = 9 + E и упростим выражение до R = 8.

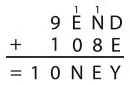
У нас остается:

E + 1 = N

D + E = Y + 10

Цифры 0 и 1 уже использовались, значит, Y должно быть равным 2 или больше. Следовательно, D + E ≥ 12. Поскольку 9 и 8 уже задействованы, единственно возможные цифры для D и E – либо 6 и 7 (или наоборот), либо 5 и 7 (или наоборот).

Предположим, что это 6 и 7. E – это или 6, или 7. Но мы пришли к противоречию, так как E + 1 = N, а значит, N тоже равно 7, а разные буквы, по условиям задачи, не могут обозначаться одной цифрой. С другой стороны, если E = 7, то уравнение E + 1 = N говорит нам о том, что N = 8, но 8 уже занято буквой R.

Таким образом, D и E – это либо 5 и 7, либо 7 и 5.

Но E не может быть равным 7 по той же причине, что и выше, иначе это означало бы, что N = 8, а это невозможно. Получается, D = 7, E = 5, Y = 2 и N = 6.

К тексту

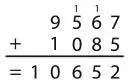
Шаг 1. Буква T должна обозначать 1, поскольку сумма двух шестизначных чисел равна семизначному числу, которое начинается с 1. (Здесь мы можем не принимать во внимание роль четырехзначного числа, так как оно не может превратить общую сумму в семизначное число, начинающееся с цифры 2 или больше. Учитывая, что каждая буква представляет отдельную цифру, максимальное значение для DOUBLE + DOUBLE + TOIL – 987 543 + 987 543 + 6824 = 1 981 910.)

Шаг 2. Решение головоломок из разряда альфаметики требует повышенного внимания к переносу чисел. В каждом столбце может быть цифра 1, перенесенная из столбца справа. А при сложении в каждом столбце может получиться цифра 1, которую следует перенести в столбец слева.

Рассмотрим столбец, соответствующий разряду тысяч. Нам нужно сложить U + U + 1 (вместе с возможным переносом из суммы в столбце сотен), а ответ должен равняться числу, в котором есть буква U в столбце единиц.

Методом исключения можно сделать вывод, что буква U может обозначать только 8, если есть перенос, поскольку 8 + 8 + 1 + 1 = 18, или 9 – если переноса нет, так как 9 + 9 + 1 = 19. В обоих случаях 1 переносится в столбец 10 тысяч.

Шаг 3. Теперь проанализируем столбец 10 тысяч. Мы знаем, что сумма O + O + 1 равна числу, в столбце единиц которого есть О. Единственно возможное значение – О = 9, притом что 1 переносится в столбец сотен. А поскольку цифра 9 теперь занята, U = 8; согласно нашим вычислениям, перенос требуется и в столбце тысяч.

Шаг 4. В столбце сотен в ответе есть буква В в разряде единиц. И есть две возможные суммы – либо B + B + 9, либо (если в этом столбце есть перенос) B + B + 9 + 1. В первом случае В – это 1, а во втором В – 0. Поскольку буква T представляет 1, буква В должна иметь значение 0, и в этом столбце есть перенос 1.

Шаг 5. Значение D должно быть больше 5, но это не может быть 5, иначе R = 1, а это число уже занято. Следовательно, D и R могут иметь только такие значения: D = 6 и R = 3 или D = 7 и R = 5.