А что, если A займет любое другое место. Предположим, место посетителя N, который занимает n -е место в очереди.
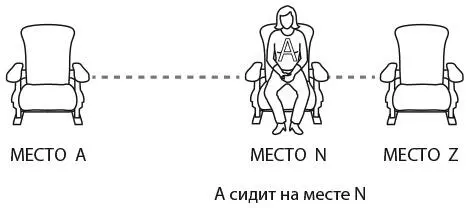
Если A сидит на месте N, то все люди, которые стоят в очереди до N, займут места, указанные в их билетах. Первым, кто не сядет на свое место, будет N, поскольку его место уже занял A. В итоге N выберет одно из оставшихся мест.
Теперь N может расположиться на месте A и местах тех, кто стоит в очереди после него, в том числе Z. Следовательно, N займет либо место A (в таком случае Z в итоге сядет на правильное место), либо место Z (в этом случае Z не сядет на свое место). Или же N сядет на место M, где M – зритель, который стоит в очереди после N, но раньше Z.
Если ограничиться размышлениями о том, займет ли N место A или Z, шансы в обоих случаях равны, а значит, Z займет свое место с вероятностью 50 процентов. А что, если N сядет на место M?
Когда наступит очередь посетителя M занять свое место, он столкнется с таким же выбором, что и N: у него есть равные шансы занять либо место A, либо место Z или шанс занять место того посетителя театра, который еще должен войти в зал. Если M займет место еще не вошедшего посетителя, сценарий повторится.
На каждом этапе любой зритель выберет либо место A, либо место Z с равной вероятностью. А если этот зритель выберет чье-то место, то решение о выборе между A и Z откладывается до следующего, кто войдет в зал. В конечном счете мы переберем всех, и кому-то придется сесть либо на место A, либо на место Z.
У любого посетителя театра, вынужденного сесть на случайное место, всегда равные шансы выбрать место A или место Z. В случае выбора места A посетитель Z займет свое место, а при выборе места Z – не свое. Таким образом, вероятность того, что Z сядет на свое место, составляет 50 %.
К тексту
10 УВЛЕКАТЕЛЬНЫХ ГОЛОВОЛОМОК
ХОРОШО ЛИ ВЫ ЗНАЕТЕ ГЕОГРАФИЮ?
1. Рим.
К тексту
2. Мэн, поскольку североатлантическое побережье США простирается на восток дальше, чем кажется.
К тексту
3. Глазго, Плимут, Эдинбург, Ливерпуль, Манчестер.
К тексту
4. Париж, Сиэтл, Галифакс, Алжир, Токио.
К тексту
5. Остров Пасхи, Перт, Кейптаун, Буэнос-Айрес, Монтевидео.
К тексту
6. Германия. У этой страны девять соседей (по часовой стрелке): Дания, Польша, Чехия, Австрия, Швейцария, Франция, Люксембург, Бельгия, Нидерланды.
К тексту
7. В порядке возрастания численности населения: Фолклендские острова, Шетландские острова, остров Мэн, Джерси, остров Уайт.
К тексту
8. Канада.
К тексту
9. Интересно, что один часовой пояс задекларирован в Китае, хотя протяженность этой страны с востока на запад составляет 4828 километров, причем это расстояние больше, чем расстояние от Лондона до Москвы.
К тексту
10. Аконкагуа – 6962 метра; Мак-Кинли – 6194 метра; Килиманджаро – 5892 метра; Эльбрус – 5642 метра.
К тексту
Глава 4. Мне нужна ваша помощь, чтобы посадить 9 деревьев. Задачи с предметами
76. 6 МОНЕТ
Сначала выложите монеты в форме параллелограмма, как показано на рисунке. Каждое перемещение обозначено стрелкой.
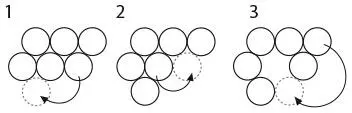
К тексту
77. ПРЕВРАЩЕНИЕ ТРЕУГОЛЬНИКА В ЛИНИЮ

К тексту
78. ВОДНАЯ ГОЛОВОЛОМКА
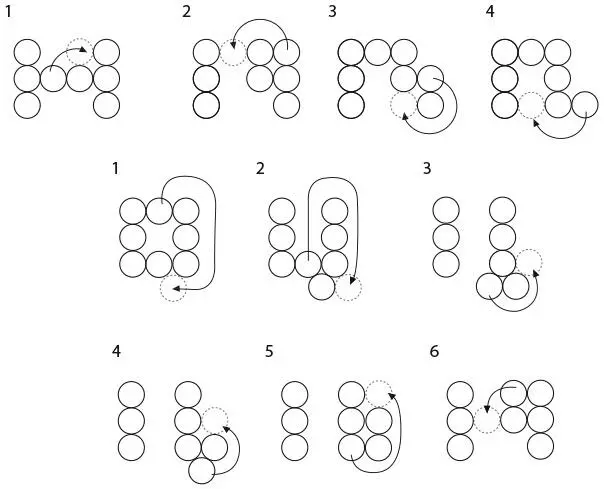
К тексту
79. 5 ПЕННИ

Решение Дьюдени состояло в том, чтобы положить одну монету горизонтально на стол, а затем еще две монеты разместить горизонтально сверху. И еще две монеты расположить так, чтобы они касались друг друга вверху и трех других монет внизу. Сделать это трудно, но возможно! В книге «Токийские головоломки» Кобон Фуджимура говорит, что один из его читателей прислал вариант решения, в котором только одна монета стоит на ребре.
К тексту
80. ПОСАДИТЕ 10 ДЕРЕВЬЕВ
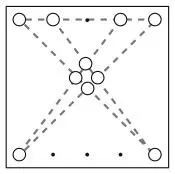
Решение начинается с двух линий, на которых расположено по пять монет; а нужно выстроить пять линий по четыре монеты в каждой.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

















