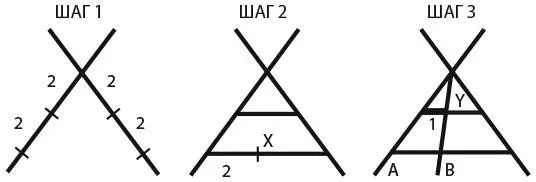Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

К тексту

2. ОДНО СЛОВО. Итак, требуется составить словосочетание «одно слово», что и получается из предложенного набора букв.

К тексту

3. С четырех согласных начинается около тридцати слов, среди них ВЗГЛЯДи ВСКРИК(все остальные подобные слова также начинаются с «вз» или «вс»). Заканчивается четырьмя согласными только одно слово – МОНСТР.

К тексту

4. Май, Июнь, Июль, Август, Сентябрь, Октябрь, Ноябрь, Декабрь, Январь, Февраль, Март, Апрель.

К тексту

5. Тригонометрия = ТРИ-Г-ономе- ТРИ-Я

К тексту

6. Антилопа, автомат, абрикосы.

К тексту

7. 1) МИГ – маг – май – чай – ЧАС – чад – гад – ГОД – род – рок – бок – бек – ВЕК – бек – бок – боа – бра – ЭРА.

Или после ГОД – гид – вид – вис – вес – ВЕК…

2) МИГ – мир – мор – бор – боа – бра – ЭРА.

К тексту

8. У Дженнифер в этой системе будет значение 15. Каждый слог в имени дает по 5 очков. Так как в имени Дженнифер три слога, то значение равно 15.

К тексту

9. Буква о. Если последовательность состоит из семи букв, всегда думайте о днях недели: п онедельник, в торник, с реда, ч етверг, п ятница, с уббота, в оскресенье.

К тексту

10. 1) Хочешь жить – умей вертеться.

2) Продать кота в мешке.

К тексту

Линейка позволяет рисовать прямые линии. Линейкой с расстоянием между делениями в 2 единицы можно рисовать прямые линии и отмечать отрезки длиной 2 единицы. Это все, с чем нам предстоит работать, и этого достаточно.

Наше решение основано на правиле, что две прямые, исходящие из одной точки, расходятся с постоянной скоростью. Нам необходимо найти способ измерить расстояние между двумя расходящимися прямыми, которое позволит нам построить отрезок прямой длиной в 1 единицу. Вот как мы это сделаем.

Шаг 1. Нарисуйте две пересекающиеся прямые. Это и есть расходящиеся прямые. Отметьте на них точки, расположенные ниже точки пересечения на расстоянии двух единиц. Теперь отметьте точки ниже новых точек на расстоянии двух единиц.

Шаг 2. Соедините отрезками первые две точки, а затем вторые. Вы получили два параллельных отрезка. На нижнем отрезке отметьте точку X на расстоянии двух единиц.

Шаг 3. Проведите прямую линию от точки пересечения исходных прямых до точки X. Отметьте точку Y в том месте, где эта прямая пересекается с верхним параллельным отрезком. Расстояние вдоль этого отрезка до точки Y, отмеченное на рисунке жирной линией, равно 1 единице. Мы выполнили задание.

Почему этот способ работает? Я обозначил одну из исходных прямых A, а последнюю проведенную нами прямую – B. Расстояние от прямой A до прямой B в точке пересечения равно нулю. По мере постепенного перемещения вниз по прямой B расстояние от A до B по длине любого отрезка, расположенного под определенным углом, увеличивается с постоянной скоростью. Следовательно, если отрезок AB в точке X имеет длину в две единицы, то параллельный отрезок AB в точке Y, расположенный на полпути к нему, должен быть равен одной единице [39].

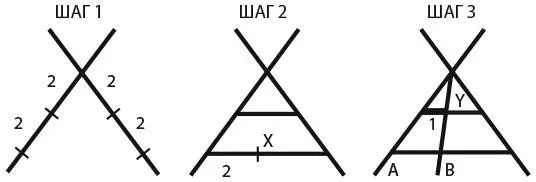
К тексту

Эту веревку можно поднять примерно на 120 метров, что почти равно высоте небоскреба Centre Point, расположенного в центре Лондона. Такое расстояние кажется парадоксально большим. У нас есть веревка длиной 40 тысяч километров, натянутая вокруг Земли; удлиненная на один метр, она поднимется так высоко, что под ней пройдет пирамида из жирафов верхом на мотоциклах, на плечах которых стоит пирамида еще из двадцати жирафов. Теперь размер Земли становится непосредственным условием для ответа.

Вычисления требуют знания тригонометрии, слишком сложной для многих читателей. Так что если вы правильно вообразили эту задачу в графическом виде и подумали над тем, как ее решить, то уже заслуживаете высокой оценки.

На представленном рисунке r обозначает радиус Земли, а h – искомое решение, то есть максимальную высоту, на которую можно поднять веревку, не растягивая. Длина отрезка веревки от максимально высокой точки до Земли обозначена буквой t , а расстояние между точками касания Земли в тот момент, когда веревка висит в воздухе, равно двум g.