Я выполню для вас эти расчеты, но нам понадобятся некоторые элементарные математические знания, а именно формула длины окружности, равная произведению радиуса и двух π , которую обычно записывают как 2 π , где π примерно равно 3,14. Надеюсь, ее введение не уведет вас в сторону от удивительного, неожиданного результата. Потерпите немного, пока я буду делать вычисления.
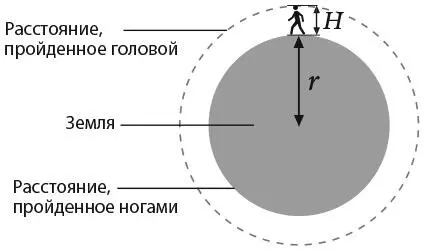
На рисунке r – это радиус Земли, а H – рост человека. По формуле длина окружности земного шара (расстояние, пройденное ногами человека) равна 2 πr , а длина окружности, обозначенной пунктиром (расстояние, пройденное головой), составляет 2 πr ( r + H ), поскольку радиус пунктирной окружности равен радиусу Земли плюс рост человека. Таким образом, разность между длинами двух окружностей, которая показывает, насколько большее расстояние проходит голова человека, составляет:
2 πr ( r + H ) – 2 πr = 2 πr + 2 πH – 2 πr = 2 πH.
Члены уравнения 2 πr сокращаются (запомните это!), а значит, ответ – 2 πH , то есть 2 × 3,14 × рост человека.
Следовательно, если рост человека равен, скажем, 1,8 метра, то его голова проходит примерно на 11 метров больше, чем ноги.
Теперь понятно, почему Уистон посчитал этот ответ достаточно интересным и достойным внимания. Это действительно крохотное расстояние, если учесть, что окружность Земли – около 40 тысяч километров. Просто невероятно, что после путешествия вокруг Земли в тысячи километров голова человека проходит всего на 11 метров больше, чем его ноги, или 0,00003 процента от пройденного пути!
Путешественник Уистона стал источником вдохновения для следующей классической головоломки.
Ответ
27. ВЕРЕВКА, НАТЯНУТАЯ ВОКРУГ ЗЕМЛИ
Допустим, вокруг земного шара туго натянута веревка. Затем ее удлинили на 1 метр и поднимали над землей до тех пор, пока она не образовала окружность, в которой каждая ее точка оказалась на одинаковой высоте от земли.
На какой высоте теперь расположена веревка? Какого размера животное может под ней пройти?
На рисунке ниже показано, что это, по сути, такая же задача, как и предыдущая. Обе подразумевают сравнение двух окружностей, меньшая из которых – окружность земного шара. В случае с веревкой длина большей окружности превышает длину меньшей окружности на 1 метр.
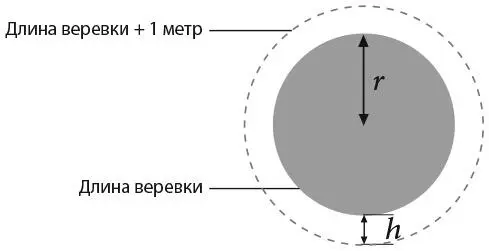
В задаче с веревкой парадоксальность ответа впечатляет еще больше. Увеличив длину веревки на 1 метр, мы сможем поднять ее над землей на 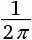 метра, то есть около 16 сантиметров. (Вот как я получил этот результат: пусть с – длина окружности земного шара, тогда длина большей веревки составит с + 1. Применив формулу длины окружности, получим два уравнения: 2 πr = c и 2 π ( r + h ) = c + 1. Эти уравнения дают 2 πh = 1 или
метра, то есть около 16 сантиметров. (Вот как я получил этот результат: пусть с – длина окружности земного шара, тогда длина большей веревки составит с + 1. Применив формулу длины окружности, получим два уравнения: 2 πr = c и 2 π ( r + h ) = c + 1. Эти уравнения дают 2 πh = 1 или 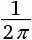 .)
.)
Поразмышляйте немного над результатом. У нас есть веревка длиной 40 тысяч километров, удлиненная до 40 001 километра. Но этого на первый взгляд несущественного увеличения достаточно, чтобы поднять ее над землей на 16 сантиметров по всей окружности земного шара. Какое животное сможет свободно пролезть под этой веревкой? Кошка или маленькая собака.
Теперь вернемся к задаче о человеке, обогнувшем Землю. При вычислении дополнительного расстояния, которое проходит его голова, мы сократили два члена уравнения 2 πr и получили 2 π , умноженное на рост человека. Важно, что радиус земного шара r отсутствует в ответе, а значит, дополнительное расстояние, преодолеваемое головой, определяется исключительно ростом человека и не зависит от радиуса Земли. Другими словами, размер планеты никак не влияет на ответ. Путешественник Уистона мог бы обойти любой шар, и в каждом случае его голова прошла бы дополнительно 11 метров.
1. Человек обходит атом. Насколько большее расстояние пройдет его голова по сравнению с расстоянием, пройденным ногами?
2. Человек обходит футбольный мяч. Насколько большее расстояние пройдет его голова по сравнению с расстоянием, пройденным ногами?
3. Человек обходит Юпитер, длина окружности которого – около 400 тысяч километров. Насколько большее расстояние преодолеет его голова по сравнению с ногами?
Читать дальше
Конец ознакомительного отрывка
Купить книгу



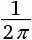 метра, то есть около 16 сантиметров. (Вот как я получил этот результат: пусть с – длина окружности земного шара, тогда длина большей веревки составит с + 1. Применив формулу длины окружности, получим два уравнения: 2 πr = c и 2 π ( r + h ) = c + 1. Эти уравнения дают 2 πh = 1 или
метра, то есть около 16 сантиметров. (Вот как я получил этот результат: пусть с – длина окружности земного шара, тогда длина большей веревки составит с + 1. Применив формулу длины окружности, получим два уравнения: 2 πr = c и 2 π ( r + h ) = c + 1. Эти уравнения дают 2 πh = 1 или 









