Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

— А не сделать ли нам статую побольше? — сказали родосцы. — Знаешь что — удвоим высоту! Сколько это будет стоить?

— В два раза дороже, конечно, — сказал Харес.

— По рукам! — сказали родосцы.

В ходе строительства Харес увидел, что его средства иссякают. Материальные издержки ошеломили его; они намного превышали отпущенный бюджет. Впереди маячило банкротство. Говорят, что Харес расстался с жизнью, чтобы избежать финансового краха, и не увидел, как был завершен его шедевр. Но, возможно, перед тем как умереть, он осознал свою ошибку.

Он постеснялся взвинтить цену.

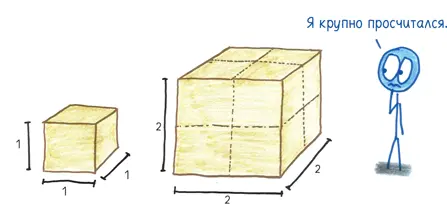
Для того чтобы понять, почему это так, забудьте все детали. Не обращайте внимания на рынок труда для греческих строителей или оптовые цены на бронзу. Черт возьми, забудьте даже об искусстве: представьте, что Харес просто строит исполинский бронзовый куб. Мы должны сосредоточиться на одном всепоглощающем вопросе: на размерах.

Что происходит, когда вы удваиваете размеры трехмерной геометрической фигуры?

Хорошо, вы удвоили длину; объем вырос в два раза. Вы удвоили ширину, и объем снова вырос в два раза. И вы удвоили высоту, удвоив объем в третий раз. Это тройной дубль, хотя не такой, как у Рассела Уэстбрука {25} 25 Американский баскетболист. — Прим. пер. : в данном случае тройное удвоение означает умножение на 8.

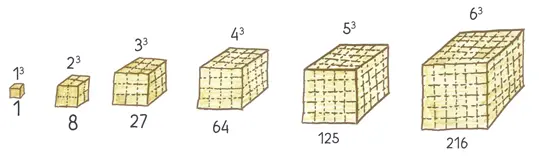
Результат настолько же ясен, насколько поразителен: объем растет с огромной скоростью.

Утраиваем стороны куба? Объем вырастает в 27 раз. Умножаем стороны на 10? Объем абсурдным образом увеличивается в 1000 раз . И то, что верно для кубов, верно для всех трехмерных геометрических фигур: пирамид, шаров, призм и (к несчастью для Хареса) роскошных статуй бога солнца Гелиоса. В точных терминах: умножьте длины сторон на r , и объем вырастет в r3 раз.

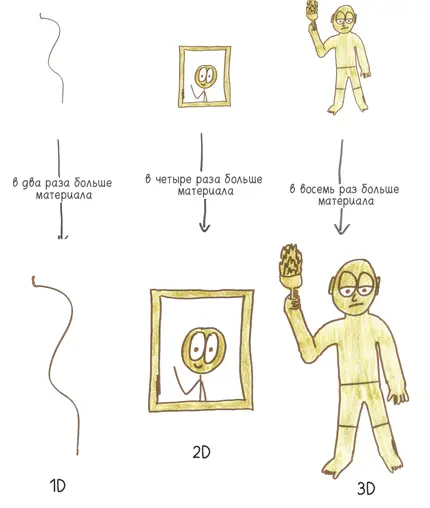
Если бы Харес создавал одномерное произведение искусства (Колоссальную Родосскую Струну) , эстетика, возможно, пострадала бы, но его ценовая политика отлично бы сработала: удваивая длину, необходимо взять в два раза больше бронзы. Или, предположим, ему было бы поручено создать двумерную картину (Колоссальный Родосский Портрет) . Цена по-прежнему осталась бы заниженной, но все же не настолько: удваивая стороны холста, мы учетверяем его площадь, поэтому требуется в четыре раза больше краски. Увы, Харес имел несчастье работать во всех трех измерениях. Удвоение высоты статуи означало, что понадобится в восемь раз больше бронзы.

Когда длины сторон растут, площадь растет гораздо быстрее, а объем — еще быстрее. Колосс Родосский — одно из чудес древнего мира — обрек своего творца на муки по той простой причине, что был трехмерным [45] Джон Коуэн (я благодарю его за сверку фактов в этой главе и за то, что он никогда не кичится и не подавляет своей эрудированностью) добавил один штрих: «На самом деле Колосс Родосский, как и статуя Свободы, был полым: бронзовые пластины и железные арматурные прутья. Следовательно, при увеличении высоты в n раз цена вырастала всего лишь в n 2 раз». Все равно чересчур для бедняги Хареса. .

Кинг-Конг, горилла размером с трехэтажный дом. Поль Баньян {26} 26 Персонаж канадского фольклора. — Прим. пер. , лесоруб, который мог перешагивать озера. Шакил О’Нил, легендарный баскетболист ростом 213 см и весом 147 кг, которому дается все, кроме штрафных бросков. Вы знаете эти истории, и вы прекрасно понимаете, что все это фантазии, легенды, наивные выдумки. Великанов не существует [46] Впервые я узнал об этом в колледже из курса Лори Сантос «Секс, эволюция и человеческая природа». Нет, я, конечно, уже знал, что великанов не существует, но объяснения профессора Сантос (возможно, как я сейчас вижу, вдохновленные Холдейном) помогли сформировать костяк этой главы. .

Почему? Потому что размер имеет значение.

Предположим, мы возьмем в качестве образцового человеческого экземпляра Дуэйна Джонсона {27} 27 Американский рестлер и киноактер ростом около 2 м. — Прим. пер. и удвоим его размеры. Если мы удвоим его вдоль, поперек и в высоту, общая масса тела Дуэйна вырастет в восемь раз.