Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Эта глава — небольшое собрание математических басен. Они показывают, как разные области, от кулинарии до биологии и финансирования искусства, подчиняются законам геометрии. В основе этих басен лежит одна основная идея, мораль настолько простая, что даже Эзоп не проговаривал ее вслух: размер имеет значение [42] Когда я работал над этой главой, мой коллега и образец для подражания Ричард Бриджес указал мне на прекрасное изложение тех же идей в эссе 90-летней давности. Я многое позаимствовал оттуда: J. B. S. Haldane, «On Being the Right Size», март 1926, https://irl.cs.ucla.edu/papers/right-size.pdf . .

Большая статуя — не просто увеличенная версия маленькой статуи. Это совершенно иной объект.

Мы с вами любим печь торты. Мы с гордостью месим тесто, чтобы осчастливить человечество шоколадным чудом. Духовка уже нагревается, но когда мы открываем кухонный шкаф, то неожиданно обнаруживаем, что наша форма для выпечки в два раза длиннее и шире, чем указано в рецепте из поваренной книги [43] Я пренебрегаю высотой, потому что при готовке шоколадных тортов вы никогда не заполняете форму тестом доверху. .

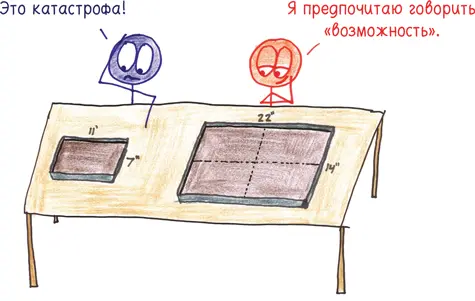
Что же нам делать?

Для того чтобы заполнить эту удвоенную форму для выпечки, у нас есть искушение взять в два раза больше ингредиентов. Но на самом деле это полумера. Посмотрите внимательнее, и вы поймете: нам необходимо учетверить количество ингредиентов.

С какой стати? Но ведь у формы два измерения: длина и ширина. Удваивая длину, мы удваиваем площадь формы. Удваивая ширину, мы снова удваиваем площадь. Таким образом, площадь удваивается дважды. Иными словами, умножается на 4.

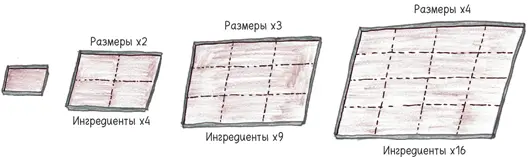
Так происходит всякий раз, когда вы увеличиваете прямоугольник. Утраиваете стороны? Площадь возрастает в девять раз. Упятеряете стороны? Площадь возрастает в 25 раз. Умножаете стороны на девять тыщмиллионов? Площадь увеличивается в 81 тыщмиллионов тыщмиллионов раз.

Или, говоря точнее: увеличивая стороны в r раз, вы увеличиваете площадь в r2 раз.

Так происходит не только с прямоугольниками. Тот же принцип работает для всех двумерных фигур: трапеций, треугольников, кругов и других емкостей, в которые вы укладываете заветное шоколадное тесто. Когда стороны увеличиваются, площадь увеличивается существенно больше.

Вернемся на кухню. Мы уже смешали вчетверо большее количество ингредиентов, когда на дальней полке обнаруживаются формы, которые мы искали все это время. Мы осыпаем друг друга упреками, но потом смеемся: кому охота пререкаться, когда скоро будет готово шоколадное великолепие?

Теперь перед нами встает выбор: готовить торт в одной большой форме или в четырех поменьше?

Это басня, поэтому мы пренебрегаем деталями. Забудьте о температуре, времени приготовления, теплопередаче и предстоящем мытье посуды. Сосредоточьтесь на одном параметре: размерах форм для выпечки.

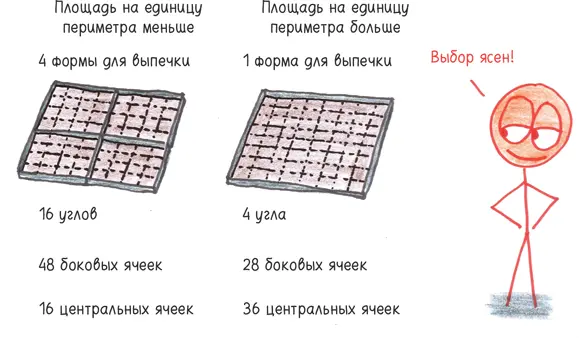
Если форма для тортов стала больше, ее периметр (одномерная величина) увеличился. Но ее площадь (двумерная величина) увеличилась еще больше. Это означает, что у четырех форм поменьше общий периметр будет больше, хотя их площадь равна площади большой формы.

У маленьких форм на единицу периметра приходится меньше площади, а у большой формы — больше.

Как я ни пытаюсь, я не могу представить себе людей, которые любят обгорелые боковушки торта. Кто променяет шоколадное чудо на пытку для зубов, хрустящее недоразумение? Мне легче представить, что они предпочитают кости вместо мяса, сухари вместо крекеров, побочные эффекты вместо обезболивающего. Этим людям нет ни объяснения, ни оправдания. Берите большую форму или расходитесь по домам.

Около 2300 лет назад жители греческого острова Родос отразили нападение Александра Македонского {24} 24 Плиний Старший пишет, что Колосс Родосский был построен после победы над Деметрием I Македонским, внучатым племянником Александра Великого (см. «Естественная история», XXXIV, 41). — Прим. пер. . В порыве самовосхваления они поручили местному скульптору Харесу построить грандиозную триумфальную статую [44] Я узнал эту историю из книги Kitty Ferguson, Pythagoras: His Lives and the Legacy of a Rational Universe (London: Icon Books, 2010). Как и многие басни, она, скорее всего, носит апокрифический характер. . По легенде, вначале Харес планировал построить 15-метровую бронзовую скульптуру.