Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

3. Почему сухая пшеница совершенно безопасна, а пшеничная мука взрывоопасна? Потому что экзотермические химические реакции происходят на поверхности вещества, и крохотные частицы пыли имеют куда большую суммарную площадь поверхности на единицу объема площади, чем цельные колосья пшеницы.

Впервые я узнал о парадоксе Ольберса от Питера ван Доккума, который вел курс, посвященный галактикам и космологии. Если вас восторгает (или раздражает) эклектизм этой главы, то причина только в том, что я получил образование по системе свободных искусств и наук (Liberal Arts).

Я уступлю последнее слово Джону Коуэну: «Что, если между нами и звездами есть какие-нибудь Темные Вещи (планеты, пыль и т. д.)? Не станут ли некоторые звезды из-за этого невидимыми, не исчезнет ли парадокс? Нет, потому что звезды, заслоненные Темными Вещами, со временем разогрели бы их до звездной температуры, упразднив всю темноту».

E. A. Poe, Eureka: A Prose Poem (New York: G. P. Putnam, 1848). [ По Э. Эврика. Поэма в прозе (Опыт о вещественной и духовной Вселенной). Пер. К. А. Бальмонта. — М.: Эксмо,2008.]

Исторические факты, приведенные в этой главе, я почерпнул из трех источников. Перечисляю их по убыванию объема позаимствованной информации:

• Deborah J. Bennett, Randomness (Cambridge, MA: Harvard University Press, 1998).

• «Rollin’ Bones: The History of Dice», Neatorama , August 18, 2014. Из книги Uncle John’s Unsinkable Bathroom Reader , https://www.neatorama.com/2014/08/18/Rollin-Bones-The-History-of-Dice/.

• Martin Gardner, «Dice», in Mathematical Magic Show (Washington, DC: Mathematical Association of America, 1989), 251–62.

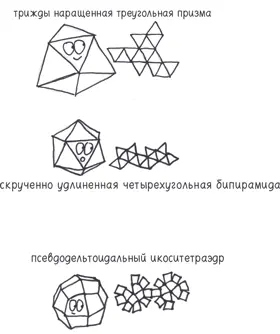
У курносого дисфеноида есть два кузена: грани этих полиэдров — равносторонние треугольники, но одни грани все равно будут выпадать чаще, чем другие: (1) трижды наращенная треугольная призма (спасибо за подсказку Лоуренсу Рэкхему) и (2) скрученно удлиненная четырехугольная бипирамида (спасибо за подсказку Тиму Кроссу и Питеру Оллису). Если вы предпочитаете четырехугольные грани, есть и (3) псевдодельтоидальный икоситетраэдр (спасибо за подсказку Александру Мюницу).

Честно говоря, прецеденты имеются. Древние жители долины реки Инд использовали треугольные продолговатые игральные кости, слепленные из глины. Их современники в Индии использовали прямоугольные параллелепипеды, выточенные из слоновой кости.

Возможно, это обстоятельство объясняет, почему все современные продолговатые игральные кости, которые мне довелось увидеть, или (1) крошечные, или (2) перекручены так, чтобы длинные грани оставались эквивалентными, обеспечивая удовлетворительное, сдержанное кувыркание. The Dice Lab (Лаборатория игральных костей), чья работа помогла мне найти вдохновение для этой главы, продает несколько симпатичных экземпляров второго вида.

Подробнее этот аргумент изложен здесь: Persi Diaconis and Joseph B. Keller, «Fair Dice», American Mathematical Monthly 96, no. 4 (April 1989): 337–39. http://statweb.stanford.edu/~cgates/PERSI/papers/fairdice.pdf.

Тем не менее некоторые цивилизации предпочитали этот способ. Древние инуиты кидали игральные кости в виде стульев, учитывая только три грани из шести. Индейцы папаго кидали кости бизонов, учитывая только две из четырех сторон.

Гениальные и зловредные подробности здесь: John Scarne, Scarne on Dice , 8th ed. (Chatsworth, CA: Wilshire Book Company, 1992).

Похожий метод, далекий от учтивости, но элегантный, использовал гангстер Большой Джул в мюзикле «Парни и куколки». На его игральных костях вообще не было точек. Но не волнуйтесь: Большой Джул прекрасно помнил, сколько точек было на какой грани.

Ну… почти. Настоящий знаток может распознать обман, потому что с определенного ракурса будет видно, что разметка граней необычная, как будто ее отразили в зеркале. По этой и другим причинам мошенники никогда не позволяют игральным костям долго оставаться в поле зрения, чтобы не попасться.

Ральф Моррисон, знаток всего обычного и необычного, рассказал мне, что Лаборатория игральных костей продает умопомрачительные 120-гранные игральные кости. Подробнее: Siobhan Roberts, «The Dice You Never Knew You Needed», Elements, New Yorker , April 26, 2016, https://www.newyorker.com/tech/annals-of-technology/the-dice-you-never-knew-you-needed.

На самом деле я почерпнул многое из книги: Ryder Windham, Chris Reiff, and Chris Trevas, Death Star Owner’s Technical Manual (London: Haynes, 2013). Я написал эту главу отчасти для того, чтобы вызвать улыбку Нейла Шепарда, но не передавайте ему мои слова.