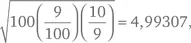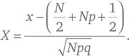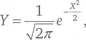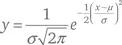В целом 3 % данных отсутствовали.
Victor Grech, Charles Savona-Ventura, and P. Vassallo-Agius, Unexplained Differences in Sex Ratios at Birth in Europe and North America, British Medical Journal 324. no. 7344 (April 27, 2002).
Persi Diaconis, Susan Holmes, and Richard Montgomery, Dynamical Bias in the Coin Toss, SIAM Review 49, no. 2 (2000): 211–235.
Robert Siegel and Andrea Hsu, What the Odds Fail to Capture When a Health Crisis Hits, NPR All Things Considered , July 21, 2014.
Протяженность дорог, согласно данным Министерства транспорта США и Федерального управления шоссейных дорог; площадь суши, согласно данным Управления лесов Министерства сельского хозяйства США.
Может показаться странным, что в 100 турах рулетки при ставке на красное вероятен выигрыш в 47 турах, а не в 50, но это происходит оттого, что p < q , поэтому максимальная вероятность отклоняется от средней.
Mazur. What's Luck Got to Do with It? 104.
Однако, чтобы уместить его на странице, график нужно сжать по горизонтальной оси, чтобы он выглядел, как график на рис. 7.4.
Мне говорили, что есть и более ранние упоминания о треугольнике, начиная с индийского математика XII в. Халаюдха, который написал комментарий к «Чанда Шастра» (трактат на санскрите, посвященный исследованию стихотворных размеров), где он отмечал, что диагонали треугольника складываются в определенные числа, которые позже назовут числами Фибоначчи. Я не встречал достоверных подтверждений тому, что подобный треугольник упоминается так рано, хотя это вполне возможно. Если это так, то там наверняка не приводится формула построения, а просто дается список достаточно большого числа рядов, чтобы им можно было пользоваться.
Петер Апиан был немецким гуманистом, математиком и астрономом. См.: D. E. Smith, History of Mathematics (New York: Dover, 1958), 508.
Mazur, What's Luck Got to Do with It? 239.
Сначала мы сдвигаем весь график так, чтобы высшая точка располагалась на 0. Очевидно, что площадь остается прежней, никакая информация не теряется, за исключением того, что теперь мы интерпретируем смысл графика как распределение вероятностей пошагового увеличения или уменьшения красного против черного. Еще одно изменение нашего рисунка – мы сжимаем кривую в 5 раз по горизонтали и растягиваем во столько же раз по вертикали. Коэффициент 5 получен в результате вычисления √ Npq , где N – это число туров, p – вероятность того, что выпадет красное, а q – вероятность того, что красное не выпадет. Точное число – 4,99307. Я округлил его до 5 для удобства использования.
Сначала надо переместить кривую так, чтобы ее среднее значение стало менее 50, затем нам необходимо вычислить скаляр (коэффициент масштабирования), на который мы будем сжимать кривую по горизонтали и растягивать по вертикали. Перемещение было нужно потому, что мы знали, что всего в игре было 100 туров.
Скаляр – это 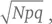 где N – число туров, p – вероятность успешного испытания, а q – вероятность неудачи ( q = 1 – p ). Другими словами, скаляр для нашей конкретной игры (ставка на красное на рулетке):
где N – число туров, p – вероятность успешного испытания, а q – вероятность неудачи ( q = 1 – p ). Другими словами, скаляр для нашей конкретной игры (ставка на красное на рулетке):
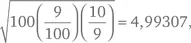
или приблизительно 5.
В общем, можно представить проделанные нами масштабирование и преобразования просто как трансформацию переменных x и y в новые переменные X и Y . Положим, X = x – a, сдвигая график как целое на a единиц вправо. Пусть X = x / b , что соответствует растяжению по горизонтали в b раз. Также положим Y = cy, чтобы отмасштабировать график по вертикали в c раз. В итоге получаем новый график: Y vs. X. Для биномиального распределения частот, где p достаточно близко к q , мы преобразуем x в X , приняв его за
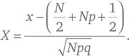
Кривая, описываемая графиком
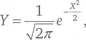
называется кривой нормального распределения и на самом деле упоминается еще у Муавра и Лапласа. Получается из нормального распределения
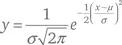
при μ = 0, σ ² = 1 (μ – это среднее, σ – стандартное отклонение).
Читать дальше
Конец ознакомительного отрывка
Купить книгу

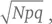 где N – число туров, p – вероятность успешного испытания, а q – вероятность неудачи ( q = 1 – p ). Другими словами, скаляр для нашей конкретной игры (ставка на красное на рулетке):
где N – число туров, p – вероятность успешного испытания, а q – вероятность неудачи ( q = 1 – p ). Другими словами, скаляр для нашей конкретной игры (ставка на красное на рулетке):