Джозеф Мазур - Игра случая. Математика и мифология совпадения

Центральные понятия математической вероятности можно отследить уже в 1654 г. Зима в Париже была необыкновенно холодной. Даже Сена замерзла. Сообщалось, что парижане катались по реке на коньках, а на перекрестках горели костры, рядом с которыми священники раздавали беднякам хлеб. Экономика была задушена 30 годами религиозных войн в Европе, опустошившими французскую казну. Государство было вынуждено повысить налоги на рабочий класс, но бесчестные сборщики налогов мало что доносили до казны. На троне восседал Людовик XIV, а знать, освобожденная от налогообложения, накапливала ужасающе непомерные богатства. Не случайно праздные богачи открыто предавались азарту в игровых залах по всему Парижу {40}. Как не случайно и то, что нарождающаяся математическая теория вероятностей появилась именно тогда, в ту самую зиму 1654 г.

Несмотря на то что азартные игры известны с начала времен или по крайней мере с тех пор, когда троглодиты стали катать кости по полу своих пещер, к середине XVII в. они стали основным видом развлечений во Франции. Серьезной математической теории случайного не существовало, кроме грубых попыток, которые мы находим в ошибочных математических работах и книге Фра Лука Пачоли «Сумма» ( Summa ), опубликованной в 1494 г., – учебнике, в основном посвященном алгебре. К 1654 г. рукопись Кардано «Книга об азартных играх» вышла в свет с некоторыми подсказками по поводу того, сколько раз нужно бросить пару игральных костей, чтобы иметь шансы на комбинацию из двух шестерок выше, чем один к одному {41}.

Философ-математик Блез Паскаль прочел экземпляр «Книги об азартных играх» в поисках этого числа, но не поверил в приведенное решение. Он заболел и пролежал в постели весну и лето, ведя переписку со своим другом, юристом и математиком Пьером Ферма {42}. Вместе они пришли к выводу, что шансы выбросить две шестерки немного меньше, чем 1 к 1, при 24 попытках и немного больше при 25.

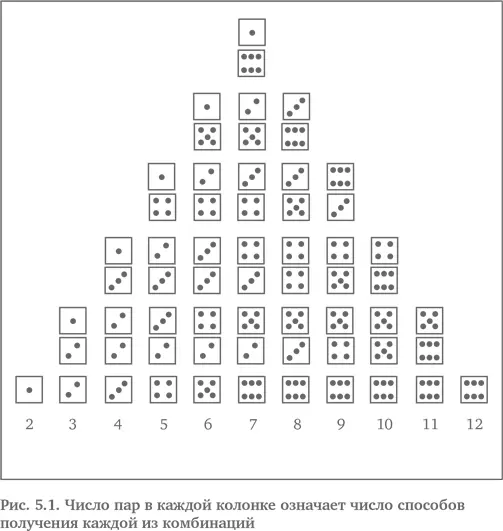
Паскаль знал, что «глаза змеи» (две единицы) и «товарные вагоны» (две шестерки) появляются очень редко, поскольку шанс их выбросить – 1 к 36, тогда как шанс выбросить семерку – 1 к 6 (рис. 5.1). Он понял, что проще будет вычислить шанс не выбросить две шестерки, т. е. 1 – 1/36 или 35/36. Он также понял, что каждый бросок не зависит от предыдущего и что вероятность двух независимых событий – это произведение вероятностей каждого из событий, а тогда вероятность не выбросить две шестерки за n бросков – (35/36) n . Он вычислил, что (35/36) 24равняется 0,509, а (35/36) 25равняется 0,494, и пришел к выводу, что шанс получить две шестерки за 24 броска немного ниже, чем 1 к 1, и немного выше, чем 1 к 1, за 25 бросков {43}.

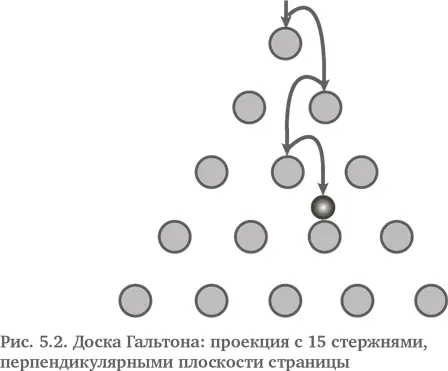
Основы учения о вероятности пришли из задачи об игральных костях и ей подобных. Внешний слой вероятностного или стохастического мира можно проиллюстрировать одной картинкой. Давайте поразмыслим о мире следующим образом: если на событие влияет некая причина, то шансы, что эта причина придаст направление возможному будущему событию, выше, чем один к одному. Если на событие не влияет никакая причина, то возможное будущее развитие события может пойти в том или ином направлении без предрасположенности к какому-либо конкретному исходу. Есть ли причина, нет ли ее – шансы выше, чем один к одному, оставляют открытой дверь для случайности или совпадения. На рис. 5.2 мы показываем это с помощью так называемой доски Гальтона в качестве модели.

Доска Гальтона моделирует события, определяемые объективной случайностью. На набор стержней бросают шарик таким образом, что шарик ударяется точно о середину верхней части стержня, при этом шансы, что шарик отскочит влево или вправо – точно 1 к 1. Если шарик отскакивает вправо, то он опускается на стержень, находящийся ниже, и либо снова ударяется точно о середину верхней его части, либо отклоняется в одну или другую сторону. В теории шарик может удариться точно о середину верхней части стержня. На практике, однако, этого никогда не происходит. Почему? Сначала мы должны задуматься: что значит «верхняя часть стержня»? Значит ли это верхнюю молекулу стали (если предположить, что стержни сделаны из стали)? Но ее не существует. Тогда на практике есть причины того, что шарик отклоняется в одну или другую сторону. Возможно, это малейший поток воздуха, через который должен пройти шарик, или малейшие колебания, проходящие через опоры стержней, или мельчайшая частичка пыли, оказавшаяся в месте соударения шарика и стержня. На практике есть сотни переменных, определяющих, в какую сторону отскочит шарик после столкновения со стержнем. Кроме того, следует учитывать микроскопические вмятины и упругость соударения.