Эдвард Шейнерман - Путеводитель для влюбленных в математику

2 × 42; 3 × 28; 12 × 7; 2 × 6 × 7; 21 × 4.

В пределе разложить на множители означает найти произведение простых чисел, например: 84 = 2 × 2 × 3 × 7. Нельзя разбить эти множители на части, потому что каждый из них представляет собой простое число. Разумеется, мы можем добавить какое-то количество единиц, например:

84 = 1 × 1 × 2 × 2 × 3 × 7,

но дополнительные множители усложняют, а не упрощают выражение, другие множители от этого не становятся меньше [16] По этой причине мы исключили число 1 из множества простых чисел. Простые числа – это неделимые кирпичики; с их помощью мы выстраиваем любое положительное целое число путем умножения. С этой точки зрения число 1 бесполезно. .

Возьмем другой пример: 120. Мы можем представить 120 как 12 × 10 и затем 12 как 2 × 2 × 3, а 10 – как 2 × 5. Это дает:

120 = (2 × 2 × 3) × (2 × 5). (A)

С другой стороны, мы можем начать так: 120 = 4 × 30 и далее заметить, что 4 = 2 × 2, а 30 = 2 × 3 × 5. Вместе это дает:

120 = (2 × 2) × (2 × 3 × 5). (B)

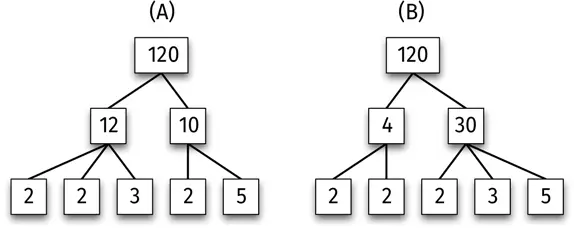
Важно отметить, что простые числа в выражениях (A) и (B) одинаковые, различается лишь порядок, в котором они перемножаются. Это показано на рисунке.

Любой способ представления числа 120 в качестве произведения простых чисел дает один и тот же результат.

Эта единственность разложения на множители зафиксирована в следующей теореме [17] Теорема – это математическое утверждение, которое может быть неопровержимо доказано. Теорема в корне отличается от научной теории, представляющей собой модель или объяснение, которое подтверждается экспериментами. Также теорема отличается от математической теории, представляющей собой совокупность определений и теорем по определенной проблематике. .

Теорема(основная теорема арифметики). Любое положительное целое (натуральное) число может быть разложено на простые множители единственным образом (если пренебречь порядком множителей) [18] Мы не даем доказательства основной теоремы арифметики. Его можно найти в большинстве книг по теории чисел – области математики, изучающей свойства чисел. .

(Здесь необходимо небольшое пояснение. В случае, скажем, числа 30 это утверждение достаточно ясно. Мы можем представить 30 как 2 × 3 × 5 или как 5 × 3 × 2 – разницы нет, отличается лишь порядок множителей. Простое число имеет всего один простой множитель – само себя. Например, множитель 13 – это 13. Но как быть с 1? Принято говорить, что пустое произведение [19] Возведение числа в нулевую степень – пример пустого произведения. По определению, 10 ⁿ представляет собой результат умножения числа 10 на само себя n раз. В случае n = 0 значение выражения 10 0 равно 1: это результат перемножения при отсутствии элементов! равно единичному элементу; таким образом, произведение отсутствующих элементов равно 1.)

Сочетая простые числа, мы выстраиваем все положительные целые числа. Простые числа – это атомы умножения.

Вернемся к вопросу: сколько всего простых чисел существует? Ответ – на следующей строчке.

Теорема. Простых чисел бесконечно много.

Утверждение приписывают Евклиду [20] Евклид – автор геометрического трактата «Начала», вершины античной математики. Его научная деятельность протекала в Александрии на рубеже IV и III веков до н. э. – Прим. пер. . Доказательство этой теоремы – математическая жемчужина. Мы не можем доказать ее методом перебора. Очевидно, что время от времени в числовом ряде попадаются простые числа. Вот несколько первых простых чисел:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61 и 67.

Но чем дальше мы идем по последовательности простых чисел, тем обширнее становятся промежутки между ними. Если посмотреть на перечень выше, можно увидеть, что два числа отстоят друг от друга максимум на 6 единиц (например, 53 и 59). Но простые числа 89 и 97 отстоят друг от друга на 8 единиц, все целые числа между ними составные. Или вот другой пример: 139 и 149 – их отделяет 10 единиц. Чем дальше мы двигаемся, тем быстрее увеличиваются промежутки между соседними простыми числами. Можно предположить, что в конечном итоге простые числа должны совсем исчезнуть. На самом деле, хотя они и встречаются все реже, их список в числовом ряду не имеет конца. Впрочем, прежде чем говорить об этом уверенно, мы должны привести доказательство.

Ключевая идея – задаться вопросом: а что, если?..