Леонид Никифоров - Математика для DATA SCIENTIST. Анализ данных и математическое моделирование (путеводитель)

© Леонид Гербертович Никифоров, 2021

ISBN 978-5-0053-4495-3

Создано в интеллектуальной издательской системе Ridero

Математика (Математическое обучение) для DATA SCIENTIST

Когда спрашивают – зачем DATA SCIENTIST’у дифференциальные уравнения, можно вспомнить графики Курта Воннегута в координатах (время по оси Х, уровень счастья-несчастья по оси Y).

https://www.youtube.com/watch?v=EEL-PIZVO08

Например, постепенное затухание жизненных сил описывается кратко и понятно одной формулой exp (-k* t), которую сразу видно на графике, где t – время, а что может быть понятнее этой переменной? Или атомный взрыв- той же экспонентой, только с положительным аргументом exp (k*t), качания на качелях или супружескую эмоциональную жизнь – одним уравнением x’' = – k*x. И траекторией y= sin (t). Как тут не вспомнить один из лучших учебников по Микроэкономике Вэриана, где автор долго и добросовестно уговаривает американцев выучить производные, чтобы одной строчкой записывать то, что иначе надо на целую страницу разъяснять.

Совсем недавно мне нужно было консультировать магистерскую диссертацию по «Применение DATA SCIENCE в классификации архетипов американских киносценариев», там была взята за основу тройка хэппи-ендов и тройка трагедий в тех же координатах, что и у Курта Воннегута.

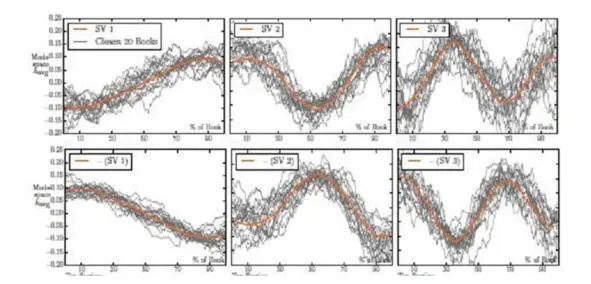
Теперь давайте предположим, что у нас есть случайная величина Z по всему сценарию как оценка (счастья-несчастья) в данный момент времени t. Ну и соответственно выборка Z (n). Как нам найти главного героя? Если есть только реплики? Я предложил ввести аналогичные Х1 (t), X2 (t) и т. д. Конечно, чтобы определить главного героя DATA SCIENCE будем вычислять ковариацию и/или корреляцию corr (Z, Xi). То есть достаточно всего одного числа – по выборке. А как определить врага главного героя? Надо искать отрицательную максимальную корреляцию. А если корреляция близка к нолю? Это кто, как вы думаете, Уважаемый Читатель? Вот вам и потребность в Теории вероятностей и Корреляционном анализе для DATA SCIENTIST.

Иногда также сомневаются в нужности Векторной алгебры и даже матриц, но это снимается теми соображениями, что бальшие массивы данных частно необходимо делить на блоки с малыми связями, как бы нарезать подмножества из всего большого множества. А также уметь смотреть под разными углами или с разных точек зрения. Но ведь это не что иное, как замена базиса пространства и определение ортогональных подпространств меньшей размерности. Вообще говоря, Линейная алгебра – должна быть в преподавании доведена до максимальной степени простоты и это только улучшает ее понимание учащимися.

Что касается предмета «Математический анализ бесконечно малых переменных величин», то мне трудно представить начинающего DATA SCIENTISTa, кто бы сомневался в необходимости этого фундаментального раздела высшей математики.

1.1 Комплексные числа. Геометрическое представление, алгебраическая и тригонометрическая форма записи, извлечение корней, корни из минус единицы.

1.2 Метод Жордано-Гаусса к системам линейных уравнений. Прямоугольные матрицы как способ представления систем линейных уравнений. Приведение матриц и систем линейных уравнений к ступенчатому виду. Самый простой и надежный метод.

1.3 Ранг матрицы. Линейная зависимость строк (столбцов). Основная лемма о линейной зависимости, базис и ранг системы строк (столбцов). Ранг матрицы. Критерий совместимости и определенности системы линейных уравнений в терминах рангов матриц. Фундаментальная система решений однородной системы линейных уравнений.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.