Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

Благодаря тесной привязке к астрономии почти вся тригонометрия оставалась сферической вплоть до 1450 г. В частности, геодезия – нынешняя главная «потребительница» тригонометрии – по сути представляет собой эмпирически разработанные методы, приведенные в систему еще римлянами. Но в середине XV в. плоскостная тригонометрия стала выделяться в отдельную отрасль знаний, и началось это в Северогерманском Ганзейском союзе. Союз контролировал практически всю торговлю, поэтому был богатой и влиятельной организацией. И ему нужны были усовершенствованные методики навигации, наряду с точным измерением времени и практической прикладной астрономией.

Ключевой фигурой того времени был Иоганн Мюллер, более известный как Региомонтан. Он был учеником Георга Пурбаха, начавшего работу над новой редакцией «Альмагеста». В 1471 г. на деньги своего патрона Бернхарда Вальтера он работает над составлением новой таблицы синусов и таблицей тангенсов.

Другие талантливые математики XV–XVI вв. сумели создать собственные тригонометрические таблицы, зачастую поражающие своей точностью. Георг Иоахим Ретик вычислил синусы для окружности с радиусом 10 15, причем очень точно, вплоть до 15-го знака после запятой, но умножал все числа на 10 15, чтобы получить целые значения – для всех кратных с шагом в одну секунду дуги. Он открыл закон для сферических треугольников:

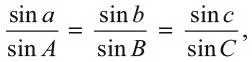
а также закон для косинусов

cos a = cos b · cos c + sin b · sin c · cos A

в своем «Трактате о сферических треугольниках», написанном в 1562–1563 гг., но опубликованном только в 1596 г. Здесь буквы A, B и C обозначают углы треугольника, при этом а, b и c – его стороны, измеренные по углам, которые они образуют с центром сферы.

Виет создал много трудов по тригонометрии, из которых первым был «Математический канон», изданный в 1579 г. Он обобщил и систематизировал разные методы решения треугольников, а именно определение длины всех его сторон и величины углов исходя из другой информации о нем. Он открыл новые тригонометрические тождества, в том числе несколько интересных выражений для синусов и косинусов углов, кратных θ, представленных через синус и косинус угла θ.

Второй темой этой главы были заявлены логарифмы, или log x , одна из важнейших функций в математике. Прежде всего они были важны, потому что удовлетворяли уравнению

log xy = log x + log y

и тем самым могли использоваться для преобразования умножения (очень трудоемкого действия) в сложение. Чтобы перемножить две величины x и y , сперва надо найти их логарифмы, сложить их и затем найти число, логарифм которого является результатом этого сложения ( антилогарифм ). Это и будет произведение ху .

Как только математики составили таблицы логарифмов, они стали доступны любому, кто знаком с методом. С XVI в. вплоть до середины XX в. практически все научные вычисления, особенно астрономические, использовали логарифмы. Однако уже с 1960-х электронные калькуляторы и компьютеры потеснили логарифмы, сделали их ненужными. Но сама концепция остается жизненно важной для математики: логарифмы прочно занимают ведущие роли во многих отраслях этой науки, включая исчисление и комплексный анализ. Кроме того, многие процессы в физике и биологии были описаны в логарифмических функциях.

Современный взгляд на логарифмы определяет их как функцию, обратную показательной. Используя логарифмы с основанием 10, что вполне естественно для десятичной системы счисления, мы говорим, что x является логарифмом y , если y = 10 x. Например, поскольку 10 3= 1000, логарифм 1000 (с основанием 10) равен 3. Главное свойство логарифмов определяется свойством показательной функции:

10 a + b= 10 a× 10 b.

Но чтобы логарифмами можно было пользоваться, необходимо уметь найти соответствующий x для всякого положительного вещественного y . Согласно утверждению Ньютона и большинства ведущих ученых того времени, главная идея состояла в том, что любое рациональное число 10 p/ qможно определить как корень q -й степени из 10 p. Поскольку любое вещественное число x может сколько угодно близко быть приближенным рациональным числом p/ q, мы можем приблизить 10 xс помощью 10 p/ q. Это не самый эффективный способ вычислить логарифм, но самый простой способ доказать его существование.