Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

Главные «потребители» алгебры в современном мире – ученые, старающиеся представить законы природы в виде уравнений. Последние могут быть решены, чтобы выразить неизвестные величины с использованием известных. Техника стала настолько привычной, что никто не замечает, что использует алгебру.

Алгебра очень эффектно была приложена к археологии в сериале «Команда времени», когда несгибаемый телеархеолог решает выяснить, насколько глубок был средневековый колодец. Первой идеей было что-нибудь туда кинуть и измерить время до момента, когда предмет упадет на дно. Это заняло шесть секунд. Соответствующая алгебраическая формула такова:

s = 1/ 2 gt 2,

где s – глубина колодца, t – время падения предмета, а g – ускорение свободного падения, примерно 10 м/с 2. Поставив 6 вместо t , по формуле мы получим глубину около 180 метров.

Из-за неуверенности в формуле – хотя, как выясняется позже, команда времени вспомнила ее правильно – герои решили опустить в колодец связанные вместе три мерные ленты.

И глубина колодца на самом деле оказалась очень близкой к 180 метрам.

Алгебра покажется нам еще более полезной, если мы будем знать глубину и захотим вычислить время. Теперь нам предстоит решить уравнение для неизвестной t с заданной s и получить результат по формуле

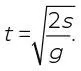
Зная, что s = 180 м, например, мы можем предположить, что t равно квадратному корню из 360/10, или квадратному корню из 36, т. е. шесть секунд.

Евклидова геометрияоснована на треугольниках – главным образом потому, что любой многоугольник можно построить из нескольких треугольников, а практически все прочие важные фигуры, такие как круги и эллипсы, аппроксимируются с помощью многоугольников. Метрические свойства треугольников – те, что поддаются измерению, например длина их сторон, величина углов или общая площадь, – описаны разными формулами, подчас весьма изящными. Практическое приложение этих формул, особенно важных для навигаторов и землемеров, дало толчок развитию тригонометрии: само название этой отрасли знаний означает «измерение треугольников».

Тригонометрия породила несколько специальных функций – математических правил для вычисления одной величины через другую. Они носят названия синус, косинус и тангенс . Тригонометрические функции стали незаменимым инструментом не только для измерения треугольников, но и для математики в целом.

Тригонометрия – наиболее широко используемый математический метод, участвующий буквально во всем: от определения местоположения корабля в навигации до работы спутниковой системы GPS в автомобилях. Ее применение в науке и технике настолько привычно, что происходит практически незаметно: такое характерно для самых универсальных инструментов. Исторически она тесно связана с логарифмами – искусным способом преобразования умножения (что достаточно трудоемко) в сложение (что намного проще). Главные идеи дисциплины были сформулированы между 1400 и 1600 гг., но она имеет длинную предысторию и массу более поздних дополнений, а ее система обозначений развивается до сих пор.

В этой главе мы проведем обзор основных тем: тригонометрические функции, экспоненциальная функция и логарифм. Также мы обратим внимание на несколько приложений, старых и новых. Многие из старых касаются техники счета и почти полностью забыты в наши дни из-за широкого применения компьютеров. Например, мало кто из наших современников до сих пор использует для умножения логарифмы. Никому не придет в голову лезть в таблицы логарифмов, раз компьютер способен моментально вычислить значение любой функции с гораздо большей точностью. Но когда логарифмы только появились, были составлены таблицы готовых расчетов из них, сделавшие их очень полезными, особенно в астрономии, где не обойтись без длинных и сложных вычислений. Составителям таблиц для нужд астрономии приходилось тратить годы – и даже десятилетия – на расчеты. Человечество очень многим обязано упорству этих преданных своему делу первопроходцев.

Главной проблемой тригонометрии было вычисление по известным данным о треугольнике (длинам сторон, величине углов) остальных его характеристик. Нам будет намного проще описать ее раннюю историю, если мы сперва резюмируем главные черты тригонометрии современной, которая по большей части является не более чем переработанной в XVIII в. областью науки, унаследованной от древних греков, если не от более ранних ученых. Краткое изложение обозначит рамки, в пределах которых мы можем описывать идеи математиков древности, не увязая в недоказуемых и со временем забытых концепциях.