Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

Эти трудности рождали все виды проблем и парадоксов. И наконец их удалось решить новой идеей анализа – понятием меры.

Специалисты по математическому анализу, работавшие над теорией интегралов, сочли необходимым пойти дальше Ньютона и дать определение еще более сложным понятиям: что представляет собой интегрируемая функция и каков ее интеграл. После ряда попыток многих предшественников Анри Лебегу удалось определить самый общий тип интеграла, сейчас известный как интеграл Лебега, со многими приятными и полезными аналитическими свойствами.

Ключом к его определению стала мера Лебега , которая представляет собой способ применить концепцию длины к весьма сложным подмножествам вещественной прямой. Предположим, множество состоит из непересекающихся интервалов с длинами 1, 1/ 2, 1/ 4, 1/ 8и т. д. Эти числа образуют сходящийся ряд с суммой 2. Здесь Лебег утверждал, что это множество имеет меру 2. В его идее обнаруживается элемент новизны: она была счетно-аддитивной . Если вы сложите бесконечный набор непересекающихся множеств и если он счетен в канторовском смысле, с кардинальным числом א 0, мера всего множества равна сумме бесконечного ряда, образованного мерами отдельных множеств.

Во многих смыслах идея меры оказалась важнее, чем интеграл, к которому она привела. В частности, вероятность и есть та же мера. На данное свойство указал в 1930-х гг. Андрей Колмогоров, составивший аксиомы для вероятностей. Точнее, он определил вероятностное пространство. В него включено множество X , набор B подмножеств X , именуемых случайными событиями , и мера m для B . Аксиомы утверждают, что m – мера и что m ( X ) = 1 (т. е. вероятность того, что что-то случится, всегда равна 1). Набор B также должен обладать теоретико-множественными свойствами, чтобы поддерживать понятие меры.

В случае с костями множество X состоит из чисел 1−6, а множество B содержит все подмножества X . Мерой любого множества Y в составе B будет количество элементов Y , деленное на 6. Эта мера согласуется с интуитивной идеей, что любая грань кости имеет вероятность выпадения 1/ 6. Однако использование меры требует от нас учитывать не только число граней, но и сами множества граней. С таким множеством Y связана вероятность того, что выпадет одна из граней множества Y . Интуитивно это будет размер Y , деленный на 6.

Благодаря этой простой идее Колмогоров положил конец спорам, в том числе вековым, и создал строгую теорию вероятностей.

Главным приложением и ответвлением теории вероятностей стала статистика, использующая вероятности для анализа данных реального мира. Она выросла из астрономии XVIII в., когда возникла необходимость учитывать ошибки наблюдений. Эмпирически и теоретически они распределены согласно функции ошибок, или нормальному распределению. Кривая этой функции формой напоминает колокол и часто называется колоколом Гаусса (колоколообразной кривой). Здесь величина ошибки откладывается по горизонтальной оси с нулевым значением посередине, а вершина кривой представляет вероятность ошибки соответствующей величины. Мелкие ошибки гораздо вероятней, серьезные случаются гораздо реже.

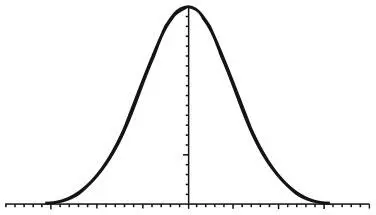
Колоколообразная кривая

В 1835 г. Адольф Кетле выступил с предложением использовать колоколообразную кривую для моделирования социальных данных: рождений, смертей, разводов, преступлений и суицидов. Он открыл, что, хотя такие события непредсказуемы для отдельных лиц, они обладают статистическими закономерностями, если рассматривать их по популяции в целом. Он воплотил свою идею, создав «среднестатистического человека», фиктивную личность со средними показателями по всем параметрам. По Кетле, среднестатистический человек вовсе не был отвлеченной математической концепцией: это объект социальной справедливости.

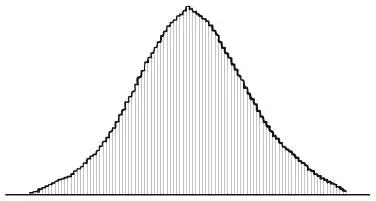
График Кетле для количества людей, имеющих данный вес. Вес откладывается по горизонтальной оси, количество людей – по вертикальной

Начиная с 1880-х общественные науки существенно расширили использование идей статистики, особенно колоколообразной кривой, в качестве замены реальному эксперименту. В 1865 г. Фрэнсис Гальтон занялся исследованием наследственности человека. Как рост ребенка соотносится с ростом его родителей? А как насчет веса или умственных способностей? Он принял колоколообразную кривую Кетле, но воспринимал ее как способ разделения определенных популяций, а не как моральный императив. Если какие-то данные демонстрировали два пика вместо одного на колоколообразной кривой, значит, популяция должна состоять из двух субпопуляций, каждая со своей кривой. К 1877 г. исследования Гальтона подвели его к изобретению регрессионного анализа – способа сравнения одного множества данных с другим для выявления наиболее вероятных взаимоотношений.