ЧТО ТЕОРИЯ ВЕРОЯТНОСТЕЙ ДАЛА ИМ
В 1710 г. Джон Арбетнот представил в Королевское общество Великобритании статью, в которой с помощью теории вероятностей доказывал существование Бога. Он проанализировал ежегодное число крещений младенцев мужского и женского пола в 1629–1710 гг. и обнаружил, что мальчиков было немногим больше, чем девочек. Более того, эта разница оставалась практически неизменной каждый год. Этот факт был уже тогда хорошо известен, но Арбетнот вычислил вероятность того, что пропорция постоянна. Его результат получился очень маленьким: 2 −82. Он указал, что если такой эффект наблюдается во всех странах, во все времена и у всех народов, то шанс был бы еще меньше. Из чего он сделал вывод, что всё происходит не по случайности, а благодаря божественному провидению.
А в 1872 г. Фрэнсис Гальтон использовал теорию вероятностей для оценки действенности молитв исходя из того, что огромное число людей каждый день возносят молитвы о здоровье королевской семьи. Он собрал данные по «средней продолжительности жизни мужчин из различных сословий, проживших более 30 лет, от 1758 до 1843 г.», добавив, что «исключил смерти от несчастного случая». В его выборку вошли аристократы, королевская семья, духовенство, адвокаты, врачи, дворяне, купцы, офицеры армии и флота, деятели науки, литературы и искусства. Он обнаружил, что «властители буквально самые коротко живущие из всех состоятельных слоев общества. Таким образом, молитвы совершенно бесполезны, если только не прибегнуть к весьма спорной гипотезе, будто условия жизни королевской семьи настолько фатальны, что отчасти, хотя и не полностью, могут нейтрализовать эффект народных молитв».
Другая базовая теорема может быть рассмотрена для случая повторных бросков бракованной (смещенной) монеты с вероятностью p для выпадения орла и q = 1 – p для выпадения решки. Если монету бросить дважды, какова будет вероятность того, что орел выпадет 2, 1 или 0 раз? Ответ Бернулли был p 2, 2 pq и q 2. Таковы результаты при разложении выражения ( p + q ) 2в p 2+ 2 pq + q 2. А если монету бросить три раза, вероятность того, что орел выпадет 3, 2, 1 или 0 раз, равна последовательности множителей в выражении ( p + q ) 3= p 3+ 3 p 2 q + 3 q 2 p + q 3.
В более общем виде, если монету бросить n раз, вероятность выпадения орла m раз будет равна:
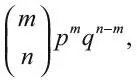
т. е. соответствующему члену в разложении ( p + q ) n.
В 1730–1738 гг. Абрахам де Муавр продолжил опыты Бернулли со смещенной монетой. Когда m и n достаточно велики, трудно точно вычислить биномиальный коэффициент, и де Муавр вывел приблизительную формулу, соответствующую биномиальному распределению Бернулли, которое сейчас мы называем функцией ошибок или нормальным распределением :
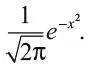
Де Муавр заслуженно считается первым математиком, явно показавшим эту связь. Это стало краеугольным камнем в развитии как теории вероятностей, так и статистики.
Основной проблемой теории вероятностей оставалось определение вероятности. Даже самые простые задачи – на которые все знают ответ – были чреваты логическими затруднениями. Если мы бросаем монету, то в длительном периоде ожидаем равного числа выпадений орлов и решек, и вероятность для каждого варианта равна 1/ 2.
Естественно, для такой вероятности монета должна быть «честной». Поврежденная может всё время выпадать орлом. Но что значит «честной»? Прежде всего, что орел и решка равновозможны. Но само выражение «равновозможны» подразумевает вероятность. Логика кажется круговой. Чтобы вычислить вероятность, нужно знать, что она собой представляет.
Чтобы выйти из этого тупика, придется вернуться к Евклиду, вдохновившему алгебраистов XIX и XX вв. Аксиомы. Хватит тревожиться о том, что такое вероятность. Запишите свойства, которыми, по вашему мнению, она должна обладать, и представьте их в виде аксиом. А потом выводите из них всё остальное.
Тогда возникает вопрос: что такое правильные аксиомы? Когда вероятность определяется по конечному множеству событий, ответить на него несложно. Однако применение теории вероятностей часто относится к потенциально бесконечному множеству возможностей. Скажем, если вы измерите угол между двумя звездами, то он будет равен некоему действительному числу между 0 и 180°. Но там бесконечно много действительных чисел. Если вы метаете дротик в доску долгое время с равным шансом попасть в любую точку на ней, то вероятность попасть в конкретную область будет равна площади этой области, деленной на общую площадь доски. Но на доске для дротиков имеется бесконечно много точек, а значит, бесконечно много областей.
Читать дальше
![Йэн Стюарт Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres] обложка книги](/books/419776/jen-styuart-ukrochenie-beskonechnosti-istoriya-matema-cover.webp)
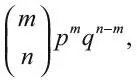
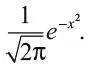





![Анна Одувалова - Высшая школа хаоса [litres]](/books/384215/anna-oduvalova-vysshaya-shkola-haosa-litres-thumb.webp)
![Ольга Пашнина - Богиня хаоса [litres]](/books/391340/olga-pashnina-boginya-haosa-litres-thumb.webp)
![Роджер Желязны - Владения Хаоса [litres]](/books/393502/rodzher-zhelyazny-vladeniya-haosa-litres-thumb.webp)
![Сара Бреннан - Дочь хаоса [litres]](/books/400527/sara-brennan-doch-haosa-litres-thumb.webp)
![Йэн Стюарт - Математика космоса [Как современная наука расшифровывает Вселенную]](/books/429584/jen-styuart-matematika-kosmosa-kak-sovremennaya-nau-thumb.webp)

