В 1843 г. к своему переводу статьи Луиджи Менабреа «Заметки об аналитической машине Чарльза Бэббиджа» Ада добавила небольшое приложение, впоследствии ставшее образцом программ, разработанных ею собственноручно. Она писала, что «отличительной особенностью аналитической машины… является использование в ней принципа управления с помощью перфокарт, изобретенного Жаккардом для изготовления самых сложных узоров для парчовых тканей. Можно сказать, что аналитическая машина сплетает алгебраические формулы так же, как ткацкий станок Жаккарда – цветы и листья».
В 36 лет у женщины развился рак матки, и после долгих мучений она умерла от кровопускания на руках у своих врачей.
Вторым важным приложением численных методов стало решение дифференциальных уравнений. Предположим, мы решаем уравнение
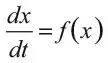
и нам дано, что x = x 0в момент времени t = 0. Согласно Эйлеру, простейший способ – аппроксимация dx / dt с помощью
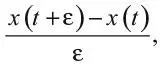
где ε очень мала. Тогда аппроксимация дифференциального уравнения принимает вид:
x ( t + ε) = x ( t ) + ε f ( x ( t )).
Начиная с x (0) = x 0мы последовательно найдем значения f (ε), f (2ε), f (3ε) – в общем, f ( n ε) для любого целого n > 0. Обычное значение ε, скажем, 10 –6. Миллион итераций (повторов) формулы покажет x (1), следующий миллион x (2) и т. д. Для современных компьютеров миллион вычислений – пустяк, и это уже вполне практичный метод.
Однако метод Эйлера оказался слишком прост для ученых, и пришлось изобрести множество улучшений. Самым известным стал целый класс методов Рунге – Кутты, названный в честь немецких математиков Карла Рунге и Мартина Кутты, впервые предложивших их в 1901 г. Один из них, так называемый метод Рунге – Кутты четвертого порядка, широко используется в инженерии, прикладной и теоретической математике.
Нужды современной нелинейной динамики породили несколько сложнейших методов, позволяющих избежать накопления ошибок даже в длительных временн ы х периодах, которые сохраняют определенную структуру, связанную с точным решением. Например, в механической системе без трения полная механическая энергия сохраняется. И есть возможность настроить численный метод так, чтобы на каждом шагу энергия сохранялась точно . Такая процедура исключает риск, что вычисленное решение будет мало-помалу отклоняться от точного, подобно тому как маятник постепенно останавливается, теряя энергию.
ЧТО ЧИСЛЕННЫЕ МЕТОДЫ ДАЛИ ИМ
Ньютону не только пришлось разобраться в природе вычислений – ему удалось изобрести эффективные методы вычислений. Он широко внедрил степенн ы е ряды для описания функций, потому что научился дифференцировать и интегрировать эти ряды одно выражение за другим. Он также использовал их для вычисления значения функций, создав один из ранних численных методов, который используется до сих пор. На одной из страниц его манускриптов, датируемой 1665 г., показано численное определение площади под гиперболой, которую мы теперь распознаем как логарифмическую функцию. Он исследовал свойства бесконечных рядов, вычислив их суммы с поразительной точностью, до 55-го десятичного знака после запятой.

Ньютоновский расчет площади под гиперболой
Более сложные структуры – симплектические интеграторы, с помощью которых решаются дифференциальные уравнения механических систем с высокой точностью, сохраняя симплектическую структуру гамильтоновых уравнений. Это любопытная, но чрезвычайно важная разновидность геометрии, адаптированная для двух типов переменных, положения и импульса. Симплектические интеграторы особенно важны для исследований небесной механики, где – например – астрономы могут захотеть отследить движения планет Солнечной системы на протяжении миллиардов лет.
Используя симплектические интеграторы, Джек Уиздом, Жак Ласкар и другие ученые показали, что в длительных временн ы х периодах поведение Солнечной системы хаотично, Уран и Нептун были гораздо ближе к Солнцу, чем сейчас, и в настоящее время орбита Меркурия смещается в сторону Венеры, так что одна из этих планет в итоге может оказаться вытесненной из Солнечной системы. Только симлектические интеграторы дают нам достаточную уверенность в том, что результаты для такого длительного промежутка точны.
Читать дальше
![Йэн Стюарт Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres] обложка книги](/books/419776/jen-styuart-ukrochenie-beskonechnosti-istoriya-matema-cover.webp)
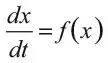
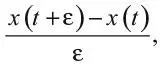






![Анна Одувалова - Высшая школа хаоса [litres]](/books/384215/anna-oduvalova-vysshaya-shkola-haosa-litres-thumb.webp)
![Ольга Пашнина - Богиня хаоса [litres]](/books/391340/olga-pashnina-boginya-haosa-litres-thumb.webp)
![Роджер Желязны - Владения Хаоса [litres]](/books/393502/rodzher-zhelyazny-vladeniya-haosa-litres-thumb.webp)
![Сара Бреннан - Дочь хаоса [litres]](/books/400527/sara-brennan-doch-haosa-litres-thumb.webp)
![Йэн Стюарт - Математика космоса [Как современная наука расшифровывает Вселенную]](/books/429584/jen-styuart-matematika-kosmosa-kak-sovremennaya-nau-thumb.webp)

