Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

Главной ошибкой здесь является восприятие математики как очевидного, буквального толкования реальности, наблюдаемой непосредственно. Но фактически мы окружены объектами, которые лучше всего будут описаны с помощью большого количества переменных, «степеней свободы» этих объектов. Например, для описания положения скелета человека требуется 100 переменных. Математически естественное описание таких объектов происходит в терминах многомерных пространств, с одним измерением для каждой переменной.

Математикам потребовалось много времени, чтобы формализовать такие описания, и еще больше на то, чтобы убедить остальных, что от этого есть польза. Сегодня всё это так глубоко вошло во все области науки, что используется практически на рефлекторном уровне. Подходы стандартны для экономики, биологии, физики, инженерии, астрономии… список можно продолжать бесконечно.

Главное преимущество многомерной геометрии в том, что человечество получило возможность визуализировать такие сверхсложные задачи, которые в принципе увидеть нельзя. А поскольку эволюционно наш мозг приспосабливался именно к визуальному мышлению, такой прием чаще приводит к неожиданным прозрениям, гораздо труднее достигаемым другими методами. Математические концепции, изначально не имеющие прямого отношения к реальному миру, часто обладают гораздо более глубокими, хотя и незримыми, связями. И эти скрытые связи делают математику такой полезной.

Прекрасный пример использования многомерных пространств – ваш мобильный телефон. То же относится к выходу в интернет, кабельному или спутниковому телевидению и практически к любой современной технологии, обеспечивающей обмен информацией. Все современные коммуникации – цифровые. Информация – даже разговоры по телефону – переводится в сочетания нулей и единиц – двоичные числа.

От коммуникаций не будет большого толку, если они ненадежны: отправленное послание должно точно соответствовать полученному. Электрические послания по проводам не могут обеспечить такую надежность из-за помех, возникающих вследствие интерференции или даже космического луча, который может вызвать ошибки. И инженерам-электронщикам пришлось прибегнуть к математическим методам для такой кодировки сигналов, где ошибки будут не только распознаваться, но и исправляться. А основой таких кодов стала математика многомерных пространств.

Такие пространства были открыты, потому что строку, скажем, из десяти двоичных чисел, или бит, такую как 1001011100, выгоднее рассмотреть как точку в десятимерном пространстве с координатами, упрощенными до 0 или 1. Многие важные вопросы о кодах, обнаруживающих и исправляющих ошибки, лучше всего решать в рамках геометрии такого пространства.

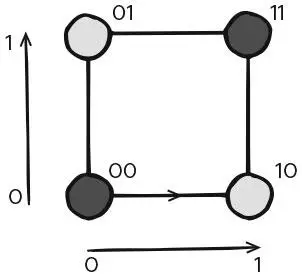
Геометрия для пары двоичных чисел

Например, мы можем обнаружить (но не исправить) одну ошибку, если закодируем каждое послание, заменяя каждый 0 на 00 и каждую 1 на 11. Тогда такое послание, как 110100, превратится в 111100110000. Если его получат в виде 11 1000110000, с ошибкой в четвертом бите, мы поймем: что-то не так, ведь выделенная жирным пара 10 не должна там присутствовать. Но нам неизвестно, должно ли это быть 00 или 11. Это можно точно проиллюстрировать на двумерной фигуре (где 2 – длина, которая соответствует кодовым словам 00 и 11). Рассматривая биты в кодовых словах как координаты, относящиеся к двум осям (соответственно для первой и второй цифр в кодовом слове), мы можем начертить схему, где настоящие кодовые слова 00 и 11 окажутся в диагонально противоположных углах квадрата.

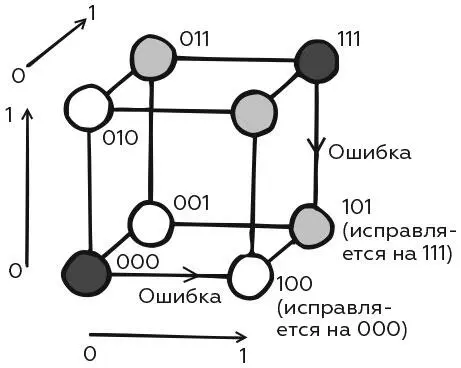
Код, исправляющий ошибки, использует строки длиной 3

Любая ошибка переведет их в кодовые слова на двух других углах – не являющиеся действительными (их мы изначально не включили в код) кодовыми словами. Но поскольку эти углы смежны с обоими настоящими кодовыми словами, разные ошибки могут привести к одному результату. Чтобы получить код, исправляющий ошибки, мы можем использовать кодовые слова длиной 3 и закодировать 0 как 000, а 1 как 111. Теперь кодовые слова находятся по углам куба в трехмерном пространстве. Любая единичная ошибка приведет в результате к соседнему кодовому слову; более того, каждое недействительное кодовое слово соседствует только с одним действительным: 000 или 111.