Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

Технические аспекты римановой геометрии многообразий, в настоящее время известной как дифференциальная геометрия, получили дальнейшее развитие в трудах Эудженио Бельтрами, Эльвина Бруно Крист о ффеля и ученых итальянской школы под руководством Грегорио Риччи и Туллио Леви-Чивита. Позже оказалось, что именно их разработок не хватало Эйнштейну для открытия его теории.

Алгебраисты тоже не сидели сложа руки, а развивали всё новые приемы вычисления для n -вариабельной алгебры – формальный символизм n -мерного пространства. Одним из таких методов стала матричная алгебра – прямоугольные массивы чисел, предложенные в 1855 г. Артуром Кейли. Такая абстракция естественным образом родилась из идеи об изменении координат. Это стало рутинным приемом – упрощать алгебраическое выражение, заменив переменные, например x и y , линейными комбинациями, например:

u = ax + by ,

v = cx + dy

для констант a, b, c и d . Кейли представил пару ( x, y ) как вектор-столбец, а коэффициенты – таблицей размера 2 × 2, или матрицей. С соответствующим определением для умножения мы можем переписать изменение координат так:

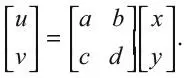
Метод легко распространяется на таблицы с любым числом строк и столбцов, представляющие линейные изменения для любого числа координат.

Примерно в 1907 г. немецкий математик Герман Минковский сформулировал теорию относительности Эйнштейна для четырехмерного пространства-времени , скомбинировав одномерное время и трехмерное пространство в единый математический объект. Он известен нам как пространство-время Минковского .

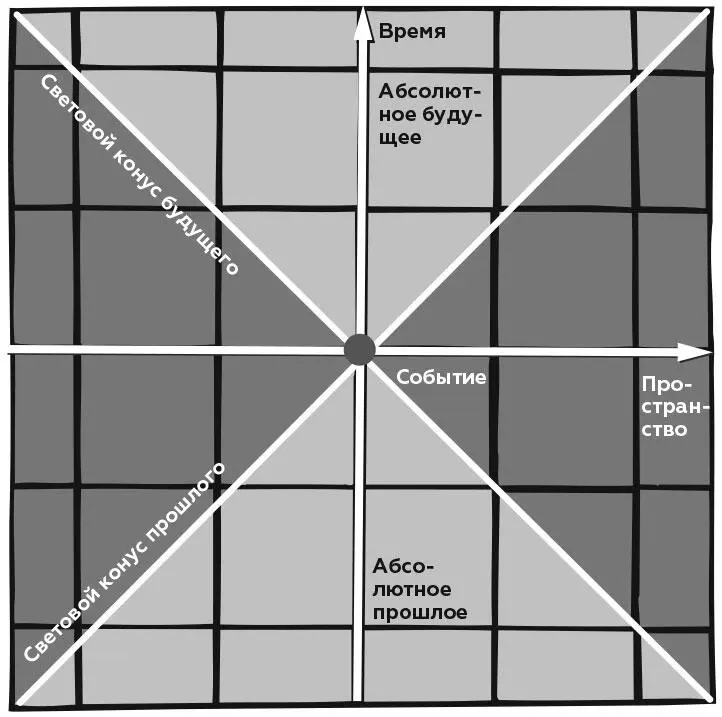
Требования теории относительности говорят, что естественная метрика пространства-времени Минковского не определяется теоремой Пифагора, в которой квадрат расстояния от точки ( x, t ) до начала координат равен x 2+ t 2. Это выражение следует заменить интервалом x 2 – c 2 t 2, где с – скорость света. Принципиальным изменением здесь является знак минус, который говорит о том, что события в пространстве-времени связаны с двумя конусами. Один (на нашей схеме это треугольник, поскольку пространство сократили на одно измерение) представляет будущее от нашего события, а другой – прошлое. Это геометрическое представление стало практически универсальным для современной физики.

Матричная алгебра позволяет делать расчеты для n -мерного пространства. По мере распространения новых идей складывался и новый геометрический язык для этого пространства, основанный на абстрактной алгебраической системе вычислений. Кейли считал свою идею не более чем удобным обозначением и предсказывал, что она никогда не получит иного применения. Сегодня эта методика распространилась во всех областях науки, особенно в такой, как статистика. Медики – одни из самых активных потребителей матриц, занимающиеся поисками статистически значимых связей между причиной и следствием.

Геометрические образы упрощают доказательство теорем. Критики утверждают, что эти новомодные геометрии относятся к пространствам, которые никогда не существовали. Алгебраисты возражают, что алгебра для n переменных существует практически наверняка, и в любом случае всякий прием, позволяющий сделать новые открытия в столь многих областях математики, заслуживает серьезного и пристального интереса. Джордж Сальмон писал: «Я уже полностью обсудил эту проблему (решения некоторой системы уравнений), когда даны три уравнения с тремя переменными. Теперь перед нами стоит вопрос о схожей задаче в пространстве с p измерениями, и мы склонны считать это чисто алгебраическим вопросом, независимым от каких-либо геометрических соображений. Но нам придется местами прибегнуть к геометрическому языку … потому что так легче понять, как применить к системе p уравнений процесс, аналогичный тому, который применили к системе из трех уравнений».

Существуют ли многомерные пространства? Конечно, ответ зависит от того, что мы подразумеваем под словом «существуют», но большинство людей не склонны вникать в такие тонкости, особенно если им что-то не нравится. Проблема стала очевидной в 1869 г. В знаменитом обращении к Британской ассоциации содействия развитию наук, позже напечатанном под заголовком «Мольба к математикам», Джеймс Джозеф Сильвестр указал, что важнейшим условием развития математики является обобщение. Ученый утверждал, что здесь главное – допустимость , а не прямое подтверждение физического опыта. Он говорил далее, что при наличии определенного навыка можно легко представить себе четыре измерения, а значит, пространство с четырьмя измерениями допустимо.