Карл Левитин - Геометрическая рапсодия

Эти плоские черви вновь возвращают нас к мозаикам — обитателям двумерного мира.

Евклидову плоскость можно покрыть квадратами так, чтобы в каждой вершине их сходилось по четыре, — это и будет мозаика {4,4}. Но стоит нам захотеть объединить квадраты таким образом, чтобы к каждой вершине прилегало лишь три из них, как фигура замкнется в пространстве и мы получим куб {4,3}. Точно так же плоскость удается заполнить правильными треугольниками, собранными по шестеркам в каждой вершине, — мозаика {3,6}. Но если надо, чтобы вершину окружали три, четыре или пять таких треугольников, то мы опять получим замкнутые пространственные тела — уже знакомые нам тетраэдр {3,3}, октаэдр {3,4} и икосаэдр {3,5}.

Размышляя об этих превращениях, мы постигаем простейшие понятия топологии. И вместе с тем становится ясным, насколько общи ее законы, насколько универсален характер изучаемых ею зависимостей.

Первым, кто увидел глубокую общность мозаик и многогранников, был Иоганн Кеплер. Именно он предложил рассматривать плоскость, заполненную прилегающими друг к другу многоугольниками, как выродившийся многогранник и потому смог применить к ним одну и и ту же общую теорию.

Потом эта его мысль была продолжена в обе стороны: жалкая многократно "надломленная" прямая линия стала выродившимся многоугольником, а многогранники превратились всего лишь в трехмерных представителей неких многомерных сверхтел — величественных "политопов", речь о которых впереди.

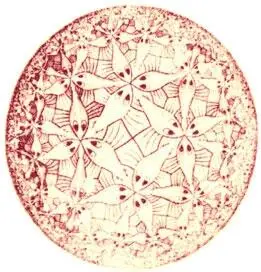
Что же касается великолепных сферических мозаик, то их положение в известном смысле промежуточное — от плоскости ушли, а к многогранникам не пришли. Но именно поэтому они оказались очень удобным инструментом для исследования пространственных фигур. Кроме того, благодаря своей броской красоте они были изучены давно — первым их описывал известный на Востоке математик Абу-л-Ваф, живший в X веке. И в наши дни сферические мозаики притягивают к себе внимание художественных натур. Например, эсхеровские "Буковый шар", "Ангелы и дьяволы" и "Сфера с человеческими фигурами" — ювелирно вырезанные из дерева пространственные мозаики так хороши, что легко могут стать источником вдохновения и фантазии.

И то и другое нам понадобится, когда речь пойдет о фигурах, живущих в четвертом и более высоких измерениях, — сверхмногогранниках.

Высшее назначение математики — находить порядок в хаосе, который нас окружает.

"Я тут не так давно разработал очень любопытный удар лапой эн в икс направлении", — говорит Дракон в пьесе Евгения Львовича Шварца. Очевидно, и омерзительный "летун-хлопотун" что-то искал в многомерном пространстве — наверное, защиту от неминуемой кары. Швейцарского математика Людвига Шлефли, символами которого мы пользовались, говоря о плоских мозаиках и трехмерных многогранниках, интересовало другое. В своей книге "Теория многократной непрерывности" он поставил такой вопрос: правильных многоугольников на плоскости может быть сколько угодно, правильных же многогранников существует только пять. Но это в пространстве трех измерений, а что будет в четвертом? Шлефли установил, что там имеют вид на жительство шесть правильных гипертел — аналогов пяти платоновых. Эти правильные сверхмногогранники, или политопы, состоят из Платоновых тел, которые называются теперь "ячейками политопа", соединенных между собой так, что каждая грань их принадлежит двум, а каждое ребро — сразу нескольким ячейкам. Если, как принято, обозначить это "нескольким" латинской буквой r, то символ Шлефли для политопа будет выглядеть так: {р, q, r}.

Что он означает, наверное, ясно.

Итак, политоп — крайний член последовательности все усложняющихся геометрических образцов: точка — линия — многоугольник — многогранник — политоп. Само это слово придумал в 1882 году Рейнгольд Хоппе — тот самый немецкий математик, что пусть с опозданием на 180 лет, но сумел рассудить спор Ньютона и Грегори, с рассказа о котором началась эта книга. Но в научный обиход оно вошло уже только в нашем веке благодаря Алисе Стотт, родной сестре Этель Лилиан Войнич, автора романа "Овод". Их отец Джордж Буль, известный математик, создатель целой науки — алгебры логики, сумел передать каждой из пяти дочерей часть своих разносторонних талантов. Алиса, например, обладала прекрасным пространственным воображением — она умела воображать четырехмерные фигуры. Сделанные ею модели политопов и по сию пору можно увидеть в Кембридже.