Джон фон Нейман (справа) и Роберт Оппенгеймер, руководитель программы по созданию первой атомной бомбы, на этой фотографии 1952 года изображены рядом с самым быстрым и точным компьютером того времени.
Абстрактная игра с чистыми стратегиями
Проанализируем более подробно игры первого типа и посмотрим, что происходит при расширении платежной матрицы, то есть в случаях, когда для каждого игрока имеется больше двух возможных ходов.
Представим следующую игру для двух игроков: игрок А выбирает строку (F1, F2, F3), его соперник — столбец (Cl, С2, СЗ) из следующей платежной матрицы, при этом ни один из игроков не знает о выборе оппонента. Выбор игроков определит элемент матрицы (он находится на пересечении выбранных строки и столбца), который укажет, сколько евро должен заплатить второй игрок первому. Как должен действовать каждый игрок, чтобы увеличить свой выигрыш или уменьшить проигрыш?
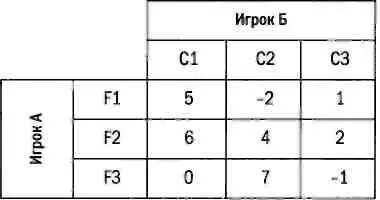
Игрок А анализирует минимальные выигрыши в зависимости от совершенных ходов. Если он выберет F1, минимальный выигрыш равен -2, 2 для строки F2 и - 1 для строки F3. Наибольший из минимальных выигрышей (максиминное значение) равен 2. Если игра является определенной, нужно выбирать строку F2. Аналогично игрок Б анализирует наибольшие проигрыши в зависимости от совершенных ходов. Если он выберет С1, максимальный проигрыш равен 6, 7 — для столбца С2 и 2 — для столбца СЗ. Наименьший из максимальных проигрышей (минимаксное значение) равен 2. Если игра является определенной, нужно выбирать столбец СЗ.
Так как в этой игре максиминное и минимаксное значения совпадают и равны 2 евро, говорят, что игра является определенной, имеет цену 2 и имеет решение в чистых стратегиях: игрок А выберет F2, игрок Б — СЗ. Также говорят, что 2 является седловой точкой, или точкой равновесия (максимальное из минимальных значений совпадает с минимальным из максимальных).
Этот пример можно обобщить для этого же числа игроков, но дав им возможность выбора не из трех, а из n ходов. Таким образом, платежная матрица будет иметь размеры n × n. Если для игры существует седловая точка, то говорят, что игра имеет точку равновесия, которой соответствует пара чистых стратегий (оптимальных для каждого игрока). Игра имеет стабильный результат, так как одностороннее изменение стратегии одним из игроков приведет к тому, что его результат станет хуже, соответственно, возрастет выигрыш оппонента.
ЯВЛЯЮТСЯ ЛИ ЭТИ ИГРЫ СТАБИЛЬНЫМИ?
Мы предлагаем читателю проанализировать матрицы следующих игр с нулевой суммой и определить, имеют ли они седловую точку.
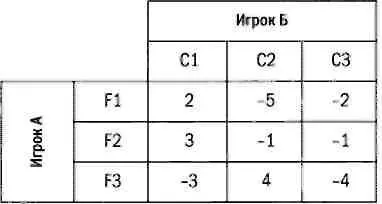
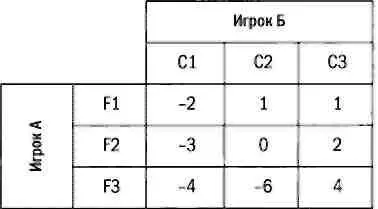
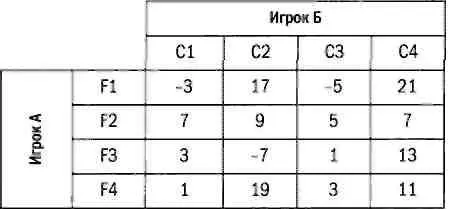
Выборы и рестораны: применение игр с чистыми стратегиями
Метод решения абстрактных игр, приведенный в прошлом разделе, можно применить в ситуациях различного рода. Рассмотрим два конкретных примера.
Представим следующую ситуацию: в некой стране во время предвыборных дебатов внимание общественности привлекла постройка объездной магистрали вокруг столицы. Имеются два варианта: трасса может пройти севернее (С) или южнее (Ю) города. Две основные партии страны, А и Б, должны определить предвыборную программу и решить, за какой из вариантов они выступают. Также они могут избежать обсуждения и никак не касаться этого вопроса в предвыборной программе. Руководство обеих партий знает, что их сторонники поддержат любое решение, но остальное население будет склоняться к тому или иному варианту, и если обе партии сделают одинаковый выбор, избиратели воздержатся от голосования. По итогам предвыборных опросов, которые известны обеим партиям, были получены следующие результаты:
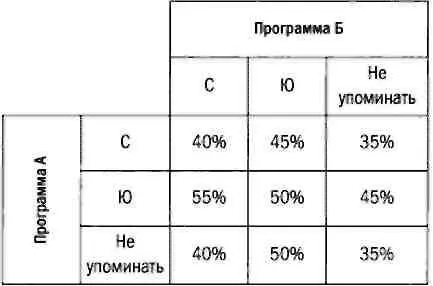
Так, если партия А предложит проложить магистраль севернее, а партия Б — южнее, партия А получит 45% голосов. Если же обе партии не будут затрагивать эту тему, партия А получит 35% голосов. Какие решения примут обе партии при заданных условиях?
Читать дальше
















