Хорди Деулофеу - Дилемма заключенного и доминантные стратегии. Теория игр

В этой главе речь пойдет об играх с нулевой суммой для двух игроков. Слова «нулевая сумма» означают, что в любой момент времени выигрыш одного игрока равен проигрышу другого. Иными словами, победитель всегда один, и он «получает все». Предполагается, что каждый игрок стремится совершить оптимальный ход, то есть тот, который сулит наибольший выигрыш. Другими словами, ни один из игроков не согласится на меньшее, чем весь выигрыш полностью.

В качестве введения в теорию игр мы расскажем о трех играх разного уровня сложности и на их примере объясним отдельные ключевые понятия, которые будут использоваться в этой и следующей главах. В этой теории применяется игровая терминология и речь идет об играх, игроках, партиях, стратегии, равновесной игре и так далее. Несмотря на это, читателю нужно понимать, что представленные задачи не обязательно соответствуют какой-либо реальной игре в том смысле, как в предыдущих главах. Нагляднее будет представлять ситуацию (противостояние) между двумя людьми или группами с установленными правилами, определяющими возможные действия. Оба игрока принимают решения одновременно (а не по очереди, как в играх, описанных в главе 2), никто из них не знает о решениях соперника. В результате принятых решений выигрывает тот или другой игрок. Далее мы будем называть подобные ситуации играми, участников будем именовать игроками. Под стратегией будем понимать решение, принятое игроком, а под выигрышем или проигрышем — последствия принятых игроками решений.

Уже в XVII веке такие ученые, как Христиан Гюйгенс (1629-1695) и Готфрид Вильгельм Лейбниц (1646-1716), предложили создать дисциплину, в которой бы использовались научные методы для изучения человеческих конфликтов и взаимодействий. Однако получить какие-либо значимые результаты по этой теме им не удалось. На протяжении всего XVIII века не было написано практически ни одной работы по анализу игр, которая бы имела подобную цель. Заслуживает упоминания письмо Джеймса Уолдгрейва от 1713 года, в котором приводится решение карточной игры для двух игроков под названием Le Her. Автор использовал способ, похожий на смешанную стратегию, и привел минимаксное решение. Несмотря на это, не было разработано ни теоретической базы, ни обобщений, чтобы подобный метод можно было применить в других случаях. В XIX веке многие экономисты создавали простые математические модели для анализа простейших конкурентных ситуаций. Среди них выделяется работа Антуана Огюста Курно «Исследование математических принципов теории богатства» (1838), в которой рассматривается случай дуополии и приводится решение, которое можно считать частным случаем равновесия Нэша. Тем не менее, теория игр как фундаментальная математическая теория появилась лишь в первой половине XX века.

Портрет Гэтфрида Вильгельма Лейбница, немецкого философа, который также занимался математикой.

Начнем рассказ об основах теории игр со следующего случая. Он очень прост и не представляет никакого интереса в качестве игры. Два игрока А и Б одновременно записывают число (1 или 2). Игрок Б должен заплатить игроку А сумму в евро, равную результату сложения двух записанных чисел. Очевидно, игра неравновесная (А всегда выигрывает), но тем не менее мы можем задаться вопросом: как должен действовать каждый игрок в соответствии со своими интересами? Для этого рассмотрим матрицу игры, так называемую платежную матрицу, в которой приведены возможные результаты:

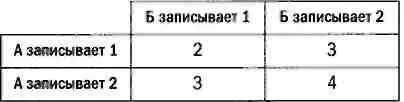
Элементы матрицы обозначают сумму в евро, которую должен заплатить игрок Б игроку А при выборе соответствующей стратегии. Каждый игрок имеет два варианта действий, поэтому всего в матрице четыре элемента. Игра очень простая, и очевидно, что, действуя согласно своим интересам, А напишет 2, Б напишет 1, выигрыш игрока А составит 3 евро.

Проанализируем ходы игроков более подробно, чтобы увидеть, каковы варианты действий для каждого игрока. А не знает, какое число записал Б, но предполагает, что Б хочет платить как можно меньше. Поэтому если А напишет 1, то выиграет минимум 2 евро, если напишет 2 — выиграет минимум 3 евро. Говорят, что 3 (число в нижней левой ячейке матрицы) — это максиминное значение (максимальное среди минимальных). Аналогично Б предполагает, что А хочет получить наибольший выигрыш. Поэтому если Б запишет 1, то потеряет максимум 3 евро, если запишет 2 — потеряет максимум 4 евро. Говорят, что в этом случае 3 является минимаксным значением (минимальным среди максимальных). Если минимаксное и максиминное значения в игре находятся в одной и той же ячейке матрицы, как в нашем случае, то говорят, что игра имеет седловую точку . (Представьте себе седло, изображенное в форме двух пересекающихся кривых, в точке пересечения которой минимальное значение одной совпадает с максимальным значением другой. Эта точка пересечения и называется седловой.)