Хорди Деулофеу - Дилемма заключенного и доминантные стратегии. Теория игр

Если руководствоваться приведенной матрицей, то выбор прост: партия А показывает наилучшие результаты, если будет поддерживать постройку трассы на юге. Именно этого варианта она и будет придерживаться. Аналогично партия Б заметит, что результаты партии А будут наихудшими (что устраивает партию Б), если Б будет избегать этой темы. Такой будет стратегия партии Б. Следовательно, игра имеет седловую точку (партия А голосует за постройку трассы на юге, Б избегает темы), цена игры — 45% голосов в пользу партии А.

Теперь предположим, что матрица имеет следующий вид:

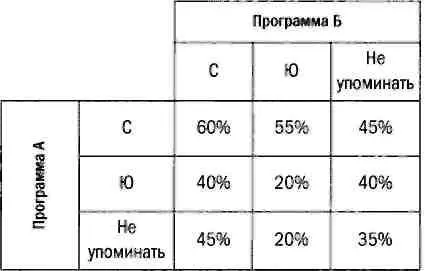
Стратегия партии А по-прежнему ясна: оптимальным вариантом в любом случае является постройка магистрали на севере. Но теперь партия Б не сможет принять оптимальное решение, не зная о выборе партии А. Выбор в пользу постройки на юге (Ю) очень привлекателен, так как в этом случае партия А может остаться лишь с 20% голосов. Однако такой выбор не имеет смысла: если партия А сделает правильный выбор, то в этом случае она получит 55% голосов, а не 20%. Поэтому для партии Б предпочтительнее не касаться этой темы, в результате партия А получит 45% голосов.

Наконец, предположим, что матрица имеет следующий вид:

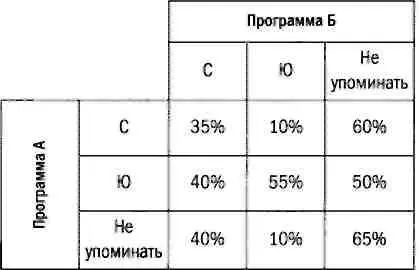
Теперь ни одна из партий не может сразу сделать выбор, так как оптимальное решение будет зависеть от того, что предпочтет оппонент. Поэтому сторонам нужно определить, какой вариант будет оптимален вне зависимости от выбора соперника. Иными словами, какой вариант — наилучший из худших. Так, если партия А выберет вариант С, то получит минимум 10%, минимум 45% — если выберет Ю, и минимум 10%, если не будет касаться этой темы. Следовательно, оптимальным вариантом является постройка трассы на юге. Аналогично если партия Б выберет вариант С, то партия А получит максимум 45%. Если партия Б выступит за постройку трассы на юге, то партии А может достаться до 55% голосов, а если партия Б уклонится от обсуждения, то партия А получит до 65%. Следовательно, партия Б должна выбрать вариант С.

В этом случае оптимальный выбор для каждой партии приводит к одинаковому результату в 45% голосов в пользу А. Эта точка является седловой, или точкой равновесия.

Двое друзей, Мария и Георгий, хотят открыть ресторан у перекрестка больших дорог за городом, который окружают горы. У них не возникло никаких разногласий, кроме одного: Мария хочет открыть ресторан в низине, а Георгий — высоко в горах, и в этом вопросе их мнения полностью противоположны. Чтобы принять решение, они придумали провести игру: друзья выбрали три параллельных автомагистрали Al, А2 и АЗ, которые идут с запада на восток, и три параллельных дороги С1, С2 и СЗ, которые идут с севера на юг. Эти дороги образуют девять перекрестков. Высота каждого перекрестка приведена в следующей матрице:

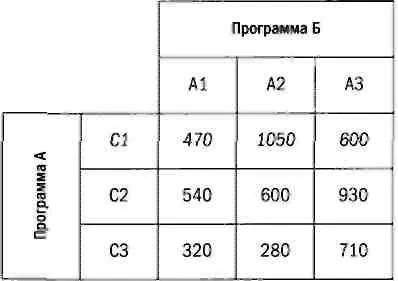
Чтобы определить место будущего ресторана, компаньоны решили действовать так: Мария выбирает одну автомагистраль (Al, А2 или АЗ), Георгий — другую (Cl, С2 или СЗ). На пересечении выбранных дорог и будет построен ресторан. Как должен действовать каждый игрок, чтобы ресторан в итоге был построен в соответствии с его интересами?

Георгий — пессимист и из трех минимальных значений (470, 540, 280) выбирает максимум. Он решает выбрать дорогу С2, что гарантирует высоту в 540 метров. Аналогично Мария оценивает максимальную высоту каждой дороги (540, 1050, 930) и выбирает трассу А1, что обеспечивает наименьшую высоту, 540 метров. Итак, оба игрока сделали свой выбор и результат в 540 метров является оптимальным для каждого из них. Иными словами, если один из компаньонов изменит свой выбор, то результат будет меньше соответствовать его интересам.

С одной стороны, эти примеры показывают разнообразие ситуаций, в которых можно найти решение, устраивающее обе стороны с противоположными интересами. С другой стороны, если матрица имеет седловую точку, то результат полностью определяется оптимальным выбором, совершенным обоими соперниками.

Многие игры и задачи, в которых используется подобная модель, нельзя решить в чистых стратегиях, так как в них отсутствует точка равновесия. Обычно для каждого игрока не существует доминантной чистой стратегии, то есть стратегии, которая каждый раз будет оптимальной. Напротив, игроки не могут раскрывать свою стратегию и всячески пытаются утаить ее от соперника, в том числе путем обмана. Например, именно так действуют игроки в покер, которые всячески стараются обмануть соперников и раскрывают свои карты только тогда, когда этого прямо требуют правила игры.