Хорди Деулофеу - Дилемма заключенного и доминантные стратегии. Теория игр

Мы определили количество групп из трех бегунов, которых можно выбрать из 12 участников забега, при этом порядок выбора имеет значение. Следовательно, тройки 1, 2, 3 и 2, 3, 1 отличаются: они образованы одними и теми же бегунами, но в первой тройке первым пришел бегун номер 1, вторым — номер 2, третьим — номер 3, а во второй тройке первым пришел бегун номер 2, вторым — номер 3, третьим — номер 1.

На языке математики это называется размещением из 12 элементов по 3 и обозначается V 12,3Как мы уже заметили, оно рассчитывается как 12 • 11 • 10. В общем виде размещение из m элементов по n (очевидно, что n < m) рассчитывается так:

V m,n= m • (m - 1) • (m - 2) • ... • (m - n + 1).

Игрок в бридж при раздаче получает 13 карт. Сколькими способами он может упорядочить карты?

Если у игрока 13 карт, то первую по порядку он может выбрать тринадцатью возможными способами, вторую — двенадцатью, третью — одиннадцатью и так далее до последней карты, которую можно будет выбрать единственным способом (она останется последней неупорядоченной). Следовательно, общее число возможных вариантов упорядочения карт равно:

13 • 12 • 11 • … • 3 • 2 • 1 = 13! = 6 227 020 800.

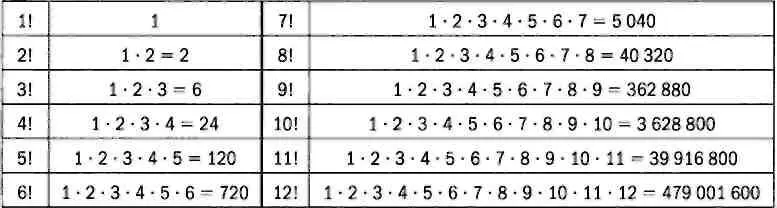
Эта операция называется перестановкой 13 элементов, и результат можно также записать в виде факториала. Факториал обозначается восклицательным знаком после числа. В нашем случае результат равен 13!. По определению n! равен произведению всех натуральных чисел от n до 1. В таблице ниже приведены значения факториала для первых 12 чисел, чтобы дать представление о том, насколько быстро он возрастает.

Подсчет лежит в основе множества карточных игр. Картина Лукаса ван Лейдена «Игроки в карты», 1520 год.

В игре бридж каждому игроку раздается по 13 карт из колоды в 52 карты. Сколькими различными способами можно выдать игроку 13 карт?

В этом случае нужно подсчитать число различных групп по 13 карт, которые можно выбрать из 52 карт, при этом порядок расположения выбранных 13 карт неважен. Если бы порядок карт имел значение, то общее число раздач вычислялось бы так:

52 • 51 • 50 • ... (13 множителей)... * 42 - 41 - 40 = 3,95424 • 10 21.

Но так как порядок карт в раздаче неважен, а каждую группу из 13 карт мы посчитали 13! раз (это число перестановок 13 элементов), число способов раздачи карт в бридже равно

(52 • 51 • ... • 41 • 40)/13! = 52!/(39! • 13!) = 635 013 559 600.

Обратите внимание, что результат выражается огромным числом. В первом случае полученное число имеет 22 цифры в своей записи, во втором (когда порядок неважен) мы получили число из 12 цифр. Это сопоставимо с возрастом Вселенной в 1,5 • 10 10лет или примерно 4,7 • 10 17секунд. Таким образом, первое число (3,9 • 10 21) более чем в 8000 раз превышает число секунд, прошедших с момента Большого взрыва, а второе число (6,3 • 10 11) в 42 раза больше возраста Вселенной в годах.

На языке математики результат этой задачи именуется числом сочетаний из 52 элементов по 13, которое обозначается С 12,13. Как мы уже видели, это сочетание рассчитывается по формуле: 52!/(39! • 13!). Общая формула для вычисления количества сочетаний из m по n (очевидно, что n < m):

С m,n= m! / (m— n)! • n!

Если финал футбольного чемпионата завершается ничьей, пробивается серия пенальти. Как правило, серия пенальти состоит из 5 ударов; все они должны выполняться разными игроками. Сколько списков из 5 пенальтистов можно составить из И игроков, которые находились на поле на момент окончания матча?

В некоторых задачах неясно, важен порядок или нет, и допускаются оба варианта. Эту задачу можно понимать двояко.

1. Нужно составить группы из 5 игроков так, чтобы любые две группы отличались между собой как минимум одним игроком. В этом случае нужно вычислить число сочетаний из 11 по 5: 11! / (5! • 6!) = 462.

2. Все интересующиеся футболом знают, что в реальности каждая команда подает арбитру пронумерованный список из 5 пенальтистов. Поэтому два списка, где указаны одни и те же игроки, но в разном порядке, будут отличаться. В этом случае нужно вычислить количество размещений из 11 по 5, равное 11!/6! = 55440.