Агниджо Банерджи - Эта странная математика. На краю бесконечности и за ним

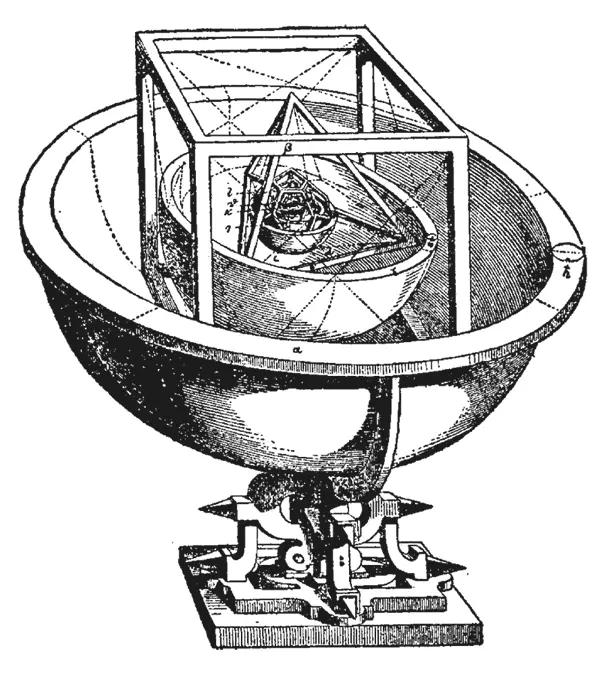
Кеплер считал, что промежутки между орбитами известных в то время планет соответствуют вложенным друг в друга платоновым телам.

Воодушевленный найденными соответствиями (которые, как выяснилось позже, были случайным совпадением), Кеплер занялся поиском менее очевидных космических гармоний. Изучив соотношения между скоростями соседних планет, он пришел к выводу, что гармоничные пропорции лежат в основе не только движения отдельных планет, но и их взаимного движения друг относительно друга. Все свои открытия ученый объединил во всеобъемлющую теорию, связывающую благозвучные интервалы в музыке с движением небесных тел, и в 1619 году обнародовал ее в главном труде своей жизни – трактате Harmonices Mundi (“Гармония мира”).

Вскоре после этого Кеплер сделал открытие, известное сегодня как третий закон движения планет, или третий закон Кеплера. Он обнаружил точное соответствие между временем, за которое планета совершает полный оборот вокруг Солнца, и ее расстоянием до светила, а именно: квадрат периода обращения планеты вокруг Солнца прямо пропорционален кубу большой полуоси ее орбиты. Этот закон и поныне входит в школьную программу, но сформулирован был в ходе мистических штудий Кеплера, искавшего гармоническую структуру космоса.

Кеплер помог вывести астрономию на современный этап ее развития, сделав важнейшее открытие: орбиты планет имеют не круговую, как считалось в древности, а эллиптическую форму. Оно заложило основу для ньютоновской теории тяготения. Менее очевидная его ценность состоит в том, что оно подготовило почву для создания новых, более гибких музыкальных строев. Проводя свои акустические эксперименты, Кеплер заинтересовался: существует ли минимальный, базовый интервал – наименьший общий делитель, – с помощью которого можно построить все остальные гармонии? Оказалось, что нет. Так же как орбиты планет представляют собой неидеальные окружности, в музыке не существует и простого, ясного способа добиться консонанса – слитного, согласного звучания, – используя лишь один базовый интервал. Особенно очевидным это становилось при попытке изменить тональность музыкальной пьесы.

Пифагоров строй, основанный на чистых квинтах, – один из примеров строя, называемого натуральным или чистым , в котором частоты нот соотносятся как довольно небольшие целые числа. Если взять, например, гамму до мажор, разделить ее на восемь ступеней разной высоты (до, ре, ми, фа, соль, ля, си, до) и присвоить тонике, или основному тону, до, соотношение 1: 1, а пятой ступени, соль, соотношение 3: 2, то в пифагоровом строе частоты нот, расположенных выше ноты до, будут относиться к ее частоте следующим образом: ре – 9: 8, ми – 81: 64, фа – 4: 3, соль – 3: 2, ля – 27: 16, си – 243: 128, до (следующей октавы) – 2: 1. Такая система прекрасно работает, если оставаться все время в той же тональности или использовать гибкий музыкальный инструмент – например, человеческий голос, – способный интонационно подстраиваться на ходу. Проблемы с любым из натуральных строев возникают при использовании таких инструментов, как фортепиано, которые, будучи настроены определенным образом, могут производить звуки только с фиксированными частотами.

Вырваться за рамки жестких ограничений пифагорова строя пытались композиторы и музыканты и до Кеплера. Но именно в его время были сделаны, по крайней мере в Европе, первые серьезные шаги в направлении полного отказа от натурального строя. Одним из пионеров этого движения стал отец Галилео Галилея Винченцо, выступавший за использование двенадцатиступенной системы, получившей название “равномерно темперированный строй”. В этой системе все соседние ноты разделены одинаковыми интервалами, то есть имеют одно и то же соотношение частот. В разделенном на двенадцать полутонов звукоряде частота каждой следующей ступени увеличивается в 2 1/12, или 1,059463, раза. Представьте себе, например, звукоряд, начинающийся с ноты ля первой октавы. Ее частота, служащая эталоном при настройке современных оркестров, – 440 герц (колебаний в секунду). Следующая нота, повыше, – ля-диез, ее частота равна 440 × 1,059463, или примерно 466,2 герца. Двенадцатью полутонами выше находится ля следующей октавы с частотой 440 × 1,059463 12 = 880 герц, то есть вдвое большей, чем у начальной ноты.

При таком построении ни один из тонов двенадцатиступенного равномерно темперированного строя, кроме тоники и октавы, по частоте не совпадает в точности с соответствующими нотами натурального строя, хотя кварты и квинты так близки к “натуральным”, что на слух их почти невозможно различить. Равномерно темперированный строй – компромисс: его ноты звучат не так чисто, как в натуральном строе, но огромное его преимущество в том, что исполняемая музыка звучит вполне гармонично в любой тональности без перенастройки инструментов. Благодаря ему такие инструменты, как фортепиано, приобрели некую практичность и музыкальную гибкость, а в музыкальной композиции и оркестровке открылись новые горизонты.