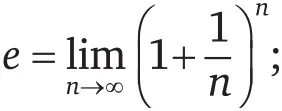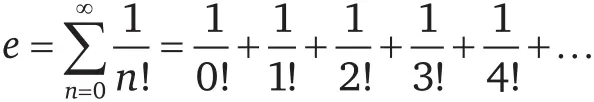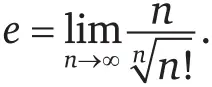Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

Число Эйлера е также не относится к алгебраическим числам, но, поскольку оно определено как предел некоторой последовательности, его значение также вычислимо, и, как и в случае числа π, есть несколько способов этого вычисления. Ниже я привожу несколько изящных и (сравнительно) простых примеров. Возможно, вы уже знакомы с первыми двумя.

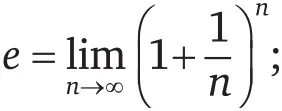
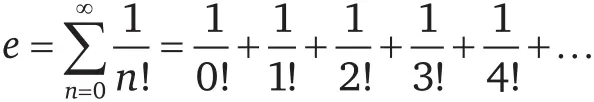
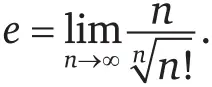
Ибо в конечном счете что же он такое – человек во Вселенной? Небытие в сравнении с бесконечностью, все сущее в сравнении с небытием, нечто среднее между всем и ничем. Бесконечно далекий от понимания этих крайностей – конца мироздания и его начала…

А существуют ли числа вещественные, но невычислимые? Они не просто существуют – их очень много. Собственно говоря, поскольку, как мы отметили раньше, количество алгоритмов счетно, мощность множества вычислимых чисел должна быть равна ℵ 0. А поскольку мощность множества вещественных чисел равна ℵ, это означает, что должно существовать ℵ вещественных чисел, которые не являются вычислимыми! Другими словами, невычислимы почти все вещественные числа. Для определения большинства вещественных чисел не существует алгоритмов. Можно ли говорить о невычислимых числах? Можете ли вы найти пример вещественного числа, которое было бы невычислимым?

Некоторые математики утверждают, что во всем наборе вещественных чисел нет необходимости, и для всех практических целей вполне можно обойтись одними только вычислимыми числами.

Тем, кто хочет узнать больше (гораздо больше!) о вычислимых числах и их интереснейшей связи с концепциями Алана Тьюринга, я настойчиво рекомендую прочитать книгу «Новый ум короля. О компьютерах, мышлении и законах физики» (1989) [59] В русском переводе эта книга была издана московским издательством «Едиториал УРСС» в 2003 г. , которую написал британский математик, философ и обладатель бесчисленных (можно ли сказать «бесконечных»?) наград и званий сэр Роджер Пенроуз.

Сэр Роджер Пенроуз разработал в сотрудничестве со своим отцом, Лайонелом Пенроузом, несколько невозможных геометрических фигур и послал их голландскому художнику М. К. Эшеру (одному из героев книги «Гёдель, Эшер, Бах»), а тот использовал их в своих гравюрах. К числу наиболее знаменитых из этих фигур относятся две следующие {34} 34 Penrose L. S. & Penrose R. Impossible Objects: A Special Type of Visual Illusion // British Journal of Psychology. 49 (1958). Р. 31–33. :

Треугольник Пенроуза

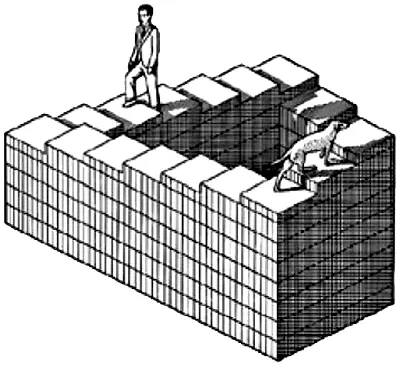
Лестница Пенроуза – нескончаемое путешествие

Только представьте себе, как вы поднимаетесь по этой лестнице – все поднимаетесь и поднимаетесь и все же все время возвращаетесь в одну и ту же точку. Эшер добавил череду вечно поднимающихся и вечно спускающихся монахов: все они оказываются в том же месте, с которого начали движение.

Ну что же, мы познакомились с несколькими интересными концепциями, но теперь нам пора вернуться к теории Кантора и узнать, что бесконечность бесконечна.

Существует ли множество чисел, мощность которого больше мощности множества вещественных чисел? Есть ли вообще «наибольшее» значение мощности?

Тот факт, что множества, имеющего наибольшую мощность, не существует, доказал сам Кантор. Собственно говоря, в этом случае доказательство Кантора было конструктивным, потому что он показал, что для любого данного множества всегда можно найти множество еще большей мощности и как это сделать. Такие множества называются показательными множествами, или булеанами.

Прежде чем мы перейдем к самой теореме, познакомимся с одной новой концепцией.

Пусть дано множество А. Множество, состоящее из всех подмножеств А, называется булеаном А и обозначается Р(А).