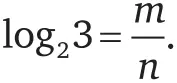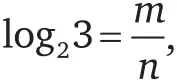Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

Попробуйте доказать, что квадратный корень из любого целого числа может быть только либо целым, либо иррациональным числом. Другими словами, квадратный корень из любого целого числа, кроме полного квадрата – 4, 9, 16, 25 и так далее, – всегда иррационален.

Ну хорошо. Когда Пифагор решил, что на свете не существует числа, квадрат которого равен 2, он слегка преувеличивал. На свете есть число, квадрат которого равен 2, и число это иррационально. Сегодня математики умеют обращаться с такими числами без особых затруднений – даже несмотря на то, что мы не можем записать их полностью. Честь основания математической теории иррациональных чисел в первую очередь следует приписать трем математикам – Рихарду Дедекинду (1831–1916), Карлу Вейерштрассу (1815–1897) и Георгу Кантору (1845–1918). Не следует полагать, что работать с такими числами легко и просто. Подумайте, например, как сложить √2 и √3 – притом что оба эти числа имеют бесконечное десятичное представление.

В самом деле, как сложить 1,41421356237309504880168872420969807… и 1,73205080756887729352744634150587236…?

Фундаментальные правила сложения, которым нас научили еще в школе, гласят, что начинать надо со сложения самых правых цифр. Но здесь мы не можем найти самые правые цифры – десятичное представление этих чисел бесконечно! Что же делать? Я же говорил вам, что не следует насмехаться над Пифагором из-за того, что он не желал считать иррациональные числа числами.

Многие считают сделанное Пифагором открытие иррациональных чисел самым важным открытием во всей истории математики {20} 20 Помимо того, что Пифагор открыл иррациональные числа, он внес еще один важный вклад в развитие математической науки: он ввел концепцию «доказательства» в смысле, очень похожем на тот, что известен нам сейчас. .

Легенда утверждает, что Пифагор велел своим ученикам хранить его открытие иррациональности длины диагонали квадрата относительно длин его сторон в секрете. Однако один из них, Гиппас, нарушил данное ему обещание (неизвестно, по каким причинам – научным или политическим) и разгласил эту тайну. Далее легенда рассказывает, что Гиппас был изгнан из сообщества пифагорейцев, а кое-кто утверждает даже, что его утопили в море (он попросту не вернулся из одного из своих плаваний вокруг греческих островов). По другой версии, иррациональные числа открыл именно Гиппас, а Пифагор не имел к этому открытию никакого отношения.

Более чем через две тысячи лет после смерти Пифагора Кантор показал, что «почти» все вещественные числа иррациональны. В число таких чисел входят и два из самых важных чисел в математике – число Эйлера e и отношение длины окружности к ее диаметру, число π.

Я обещал, что буду использовать в этой книге только четыре базовые математические операции. Но кому нужен такой «закон», который нельзя нарушить хотя бы один раз? Вот сейчас мы его и нарушим.

Числа, доказать иррациональность которых легче всего, порождаются операцией логарифмирования {21} 21 Если вы вдруг забыли, что такое логарифм, напомню, что логарифм – это функция, обратная показательной. То есть если b y = x , то log b x = y . Другими словами, логарифм данного числа x – это степень, в которую нужно возвести другое данное число, основание b , чтобы получить число x . Например, 1000 = 10³; следовательно, log 10 1000 = 3. Точно так же log 2 64 = 6, поскольку 2 6 = 64. . Например, рассмотрим log 23, то есть логарифм 3 по основанию 2. Докажем его иррациональность. Для начала предположим, что этому числу равно отношение m / n :

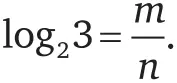
Исходя из определения логарифма и законов операций со степенями, из этого следует, что 2 m / n = 3, а (2 m / n ) n = 3 n , а следовательно, 2 m = 3 n .

Однако никакая степень 2 не может быть равна какой бы то ни было степени 3 [28] Напомним, что речь идет о степенях, являющихся натуральными числами. – Примеч. ред. : 2 в любой степени всегда дает четное число, а 3 в любой степени – нечетное. Значит, мы пришли к противоречию. Другими словами, не существует таких чисел m и n , для которых

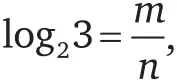
что означает, что m / n не может быть рациональным. Следовательно, log 23 – иррациональное число.

1. Докажите, что золотое сечение {22} 22 Две величины образуют золотое сечение, если их отношение равно отношению их суммы к большей из них (то есть если a > b и a / b = ( a + b )/ a , то величины a и b образуют золотое сечение). Золотое сечение обозначают буквой ϕ. ϕ [29] В русской математической литературе это число чаще обозначают прописной буквой Φ, а строчной буквой ϕ – число, обратное ему, т. е. 1/Φ. – иррациональное число.