Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

Сейчас объясню.

Начнем с квадрата, стороны которого имеют единичную длину. Обозначим длину его диагонали с :

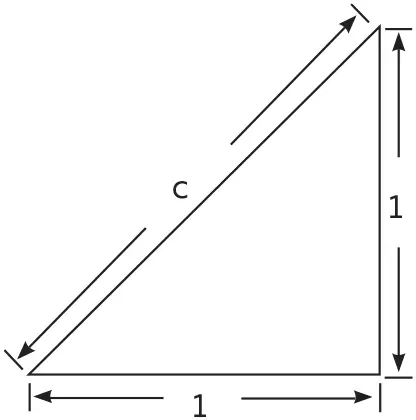
Вот что говорит теорема, прославившая Пифагора: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов двух других его сторон.

В приложении к нашему чертежу это означает, что 1² + 1² = с ², а следовательно, c = √2.

Отметим, что √2 – всего лишь символ, обозначающий число, которое, будучи умножено само на себя, дает число 2. Теоретически мы могли бы нарисовать цветок и сказать, что он обозначает число, квадрат которого равен 2. Очевидно, не существует такого целого числа, квадрат которого был бы равен 2 (поскольку 1 в квадрате равно 1, 2 в квадрате равно 4, а других целых чисел между 1 и 2 нет).

Но может ли существовать некая дробь a / b , такая, что при возведении ее в квадрат получает- ся 2? Здесь я напомню вам, что числа вида a / b , где a – целое число (которое может быть и нулем), а b – натуральное (то есть положительное целое) число, называются рациональными числами. Пифагор, несомненно, был бы очень рад, если бы такая дробь существовала, потому что это отлично согласовывалось бы с его философским воззрением, что все на свете может быть представлено натуральными числами.

Однако Пифагора ожидали чрезвычайно неприятные новости!

Сейчас мы докажем, что √2 никак не может быть выражен дробью вида a / b , где оба числа a и b – натуральные. Другими словами, мы докажем, что √2 – число не рациональное.

Для этого мы воспользуемся методом доказательства от противного, с которым мы уже встречались в этой книге. Другими словами, сначала мы предположим, что утверждение, которое мы хотим доказать, ложно, то есть что существуют такие два числа a и b, что a / b = √2. Затем мы покажем, что логические следствия из этого предположения приводят к противоречию.

Начнем наше доказательство с предположения, что a / b – приведенная дробь [27] Еще такую дробь называют несократимой. – При меч. ред. , то есть дробь, записанная с наименьшим возможным знаменателем (так, например, дроби 21/14 и 15/10 могут быть сведены к дроби 3/2). Чтобы доказать, что √2 – иррациональное число, достаточно показать, что не существует приведенной дроби, равной квадратному корню из 2. Такое дополнительное предположение относительно этой дроби пригодится нам для доказательства. Это предположение допустимо, потому что записать в приведенном виде можно любую дробь; следовательно, если не существует приведенной дроби, равной √2, то это означает, что не существует и вообще никакой дроби, которая была бы равна √2.

Итак, возьмем приведенную дробь a / b и предположим, что a / b = √2. Небольшое преобразование дает нам √2· b = a , а после возведения обеих частей этого равенства в квадрат мы получим 2 b ² = a ². Из этого явно следует, что a ² – четное число, что означает, что и число a должно быть четным. Следовательно, в предыдущем равенстве мы можем произвести подстановку a = 2 k и получим:

2 b ² = (2 k )²;

2 b ² = 4 k ²;

b ² = 2 k ².

Мы видим, что b ² – четное число, что означает, что и число b должно быть четным.

Однако если оба числа a и b – четные, дробь a / b не может быть приведенной, потому что и числитель, и знаменатель можно разделить на 2. Следовательно, мы получили противоречие с предыдущим предположением о том, что мы начали с приведенной дроби. Другими словами, мы только что доказали, что √2 не может быть отношением двух целых чисел. Вывод: √2 должен быть числом иррациональным.

Ч. т. д.

Но каково значение того утверждения, которое мы только что доказали?

С точки зрения геометрии оно означает следующее: мы легко можем построить прямоугольный треугольник с катетами единичной длины и столь же легко построить его гипотенузу, но не можем точно определить длину этой гипотенузы относительно длин двух других сторон треугольника за конечное число шагов.

Столь простая геометрическая концепция – гипотенуза треугольника – опровергает основополагающий принцип философии Пифагора, который утверждает, что всё образовано из натуральных чисел. Легко вообразить, что вместе с радостью открытия Пифагор ощутил сильнейшее разочарование.