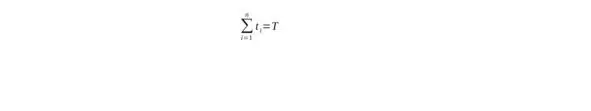Александр Берлин - Математика рынка. Обслуживание случайных потоков

Под поступающим предложением товаров за промежуток времени ( t 1, t 2) понимают предложение товаров, которое было бы обслужено рынком, если бы каждому поступающему товару сразу же был предоставлен потребитель – A пост. ( t 1, t 2). Иногда это предложение будем называть потенциальным предложением.

Разницу между поступающим и обслуженным предложением будем называть потерянным предложением 1:

A потер ( t 1, t 2) = A пост ( t 1, t 2) — A обсл ( t 1, t 2)

По аналогии с понятиями мгновенной и средней интенсивностей потоков товаров можно рассматривать мгновенную и среднюю интенсивности предложения товаров. Однако в теории и практике расчета пропускной способности рынка целесообразно использовать среднюю интенсивность предложения.

Под интенсивностью предложенияпонимается предложение товаров в единицу времени. За единицу измерения интенсивности предложения товаров принята величина a =1,т.е. предложение равное по величине максимальному ( P реал= P max).

Приведенная ниже теорема облегчает определение интенсивности обслуженного предложения.

Она показывает, что эта величина обладает свойством эргодичности, которое заключается в том, что

Среднее по времени равно среднему по ансамблю.

В данном случае наблюдение за поступлением партий товаров по времени можно заменить наблюдением числа одновременно занятых групп потребителей.

Теорема о количественной оценке интенсивности обслуженного предложения :

интенсивность обслуженного предложения, выраженная в единицах удельного относительного потребления, количественно равна среднему числу одновременно занятых групп потребителей, обслуживающих эту нагрузку.

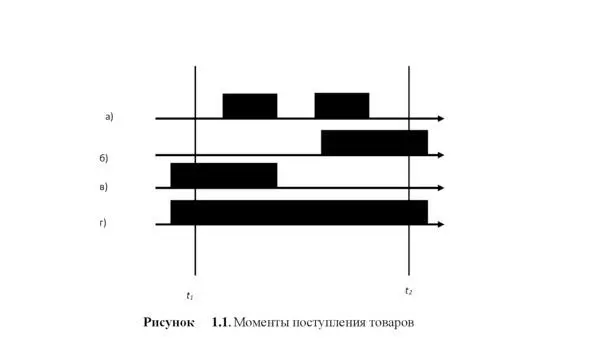
Пусть в течение Т часов непрерывно регистрируется число одновременно занятых групп потребителей рынка, которым поступает стационарный поток предложений от групп потребителей. Пусть в результате наблюдений оказалось, что в течение времени t 1было занято υ 1групп потребителей, в течение времени t 2.υ2 групп потребителей и т. д. (рис.1.1).В общем виде можно представить, что в течение времени t i была занято υi групп потребителей, причем.

Σ i=1 n t i=T

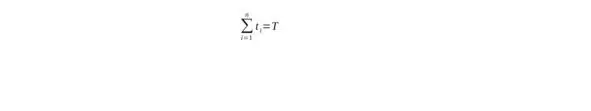
где n – число значение, которое величины υ i принимала, в течение T часов

Суммарное время занятия всех потребителей рынка за время t i выразится произведением υ it i . За промежуток времени T суммарное время занятия всех потребителей рынка выразится суммой. Эта сумма по определению является предложением, обслуженным всеми потребителями рынка за время T.

Предложение, обслуженное всеми потребителями рынка за единицу времени, будет равна:

A обсл= (Σ i=1 kv i⋅t i} 1/T

С другой стороны, среднее число одновременно занятых групп потребителей за время Т можно определить как среднее взвешенное по t i :

v= (v 1t 1+v 2t 2+…+v nt) /t1+t 2+…t n) = (1/T) (Σ i =1 nv i⋅ t -I)

,следовательно A обсл.= v »

Теорема о количественной оценке интенсивности поступающего предложения

Для количественной оценки интенсивности поступающего предложения товара можно воспользоваться следующей теоремой:

интенсивность поступающего предложения товара, выраженная в единицах относительного потребления, создаваемая простейшим потоком товаров, количественно равна математическому ожиданию числа предложений товаров (́c’), поступающих за время, равное средней длительности одного потребления одной партии товаров (́t’ потреб)

Пусть на входы рынка поступает простейший поток товаров с интенсивностью μ. Будем считать, что длительность потребления Т конечная случайная величина 0≤T≤Т maх, не зависящая от типа потока поступающих товаров, со средним значением ́t. Рассмотрим промежуток времени [ t 1, t 2) такой, что t 2 – t 1> T max. Математическое ожидание числа партий товаров, поступивших на рынок за промежуток времени

[ t 1, t 2), как Λ ( t 1, t 2) =μ ( t 2. t 1).